
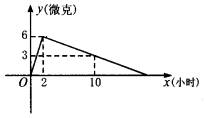
科目: 来源:数学教研室 题型:044
(1)分别求出x≤2和x≥2时,y与x之间的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上时,在治疗疾病时是有效的,那么这个有效时间是多长?
查看答案和解析>>
科目: 来源:数学教研室 题型:044
①速度v>0,表示汽车向数轴正方向行驶;速度v<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止.
②汽车位置在数轴上的坐标s>0,表示汽车位于零千米路标的右侧;汽车位置在数轴上的坐标s<0,表示汽车位于零千米路标的左侧;汽车位置在数轴上的坐标s=0,表示汽车恰好在零千米路标处.遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数图象的形式画在了同一直角坐标系中(如图).
请回答下列问题:
(1)就这两个一次函数图象所反映的两汽车在这条公路上行驶的状况填写如下的表格:

(2)甲、乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置;如不能相遇,说明理由.

查看答案和解析>>
科目: 来源:数学教研室 题型:044
(1)求这个一次函数的解析式;
(2)画出这个函数的图象;
(3)利用图象求方程(a2+b2)x-(a+b)-1=0的根;
(4)利用图象求不等式(a2+b2)x<(a+b)+1的解集;
(5)当此函数y的值在-5≤y≤3时,求x的取值范围.
查看答案和解析>>
科目: 来源:数学教研室 题型:044
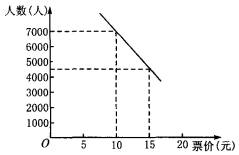
查看答案和解析>>
科目: 来源:数学教研室 题型:044
(1)设该厂向A市销售饼干为x kg,铁路运费为y1元,公路运费为y2元,分别写出两种运送方案所需费用y与x之间的表达式;
(2)当向A市销售饼干多少千克时,两种运送方案所需费用一样多?
(3)设销售的饼干重量为x kg ,试讨论哪种运送方案更合算?
查看答案和解析>>
科目: 来源:数学教研室 题型:044
查看答案和解析>>
科目: 来源:数学教研室 题型:044
查看答案和解析>>
科目: 来源:数学教研室 题型:044
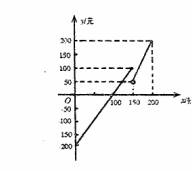
其中保险部门规定:超过150人时,要缴纳公安消防保险费50元。试根据关系图,回答下列问题:
(1) 试就0<x≤150和150<x≤200,分别写出盈利额y(元)与x(张)之间的函数关系式;
(2) 当售出的票数x为何值时,此放映体不赔不赚?当售出的票数x满足何值时,此放映体要赔本?当售出的票数x为何值时,此放映厅能赚钱?
当售出的票数x为何值时,此时所获得利润比x=150时多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com