
科目: 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:059
如图所示,有四个动点P,Q,E,F分别从面积为4的正方形ABCD的顶点A,B,C,D同时出发,沿着AB,BC,CD,DA以同样的速度向B,C,D,A移动.
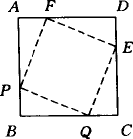
(1)证明四边形PQEF是正方形;
(2)PE是否总过某一定点?说明理由;
(3)四边形PQEF的顶点位于何处,其面积是否有最小值?最小值是多少?
查看答案和解析>>
科目: 来源:三点一测丛书 九年级数学 上 (江苏版课标本) 江苏版课标本 题型:059
已知矩形ABCD和点P,当点P在如图(1)中的位置时,则有结论:S△PBC=S△PAC+S△PCD.理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
∵S△PBC+S△PAD=![]() BC·PF+
BC·PF+![]() AD·PE=
AD·PE=![]() BC(PF+PE)=
BC(PF+PE)=![]() BC·EF=
BC·EF=![]() S矩形ABCD,又∵S△PAC+S△PCD+S△PAD=
S矩形ABCD,又∵S△PAC+S△PCD+S△PAD=![]() S矩形ABCD,
S矩形ABCD,
∴S△PBC+S△PAD=S△PAC+S△PCD+S△PAD.∴S△PBC=S△PAC+S△PCD.

请你参考上述信息,当点P分别在图(2)(3)中的位置时,S△PBC、S△PAC、S△PCD又有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明.
查看答案和解析>>
科目: 来源:三点一测丛书 九年级数学 上 (江苏版课标本) 江苏版课标本 题型:059
如图(1)、(2),四边形ABCD是正方形,M是AB延长线上的一点,直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.
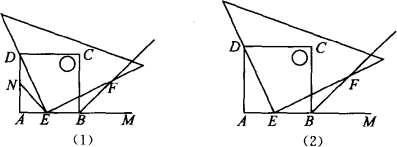
(1)如图(1),当点E在AB边的中点位置时:
①通过测量DE、EF的长度,猜想DE与EF满足的数量关系是________;
②连结点E与AD边的中点N,猜想NE与BF满足的数量关系是________;
③请证明你的上述两个猜想.
(2)如图(2),当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想此时DE与EF有怎样的数量关系.
查看答案和解析>>
科目: 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:059
阅读以下材料并填空.
平面上有n个点(n≥2),且任意三个点不在同一直线上,过这些点作直线,一共能作出多少条不同的直线?
(1)分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线;……
(2)归纳:考察点的个数n和可连成直线的条数Sn,发现:
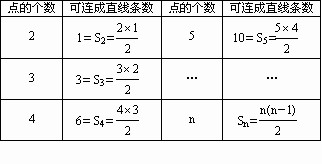
(3)推理:平面上有n个点,两点确定一条直线.取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2,即Sn=![]() .
.
(4)结论:Sn=![]() .
.
试探究以下问题:
平面上有n(n≥3)个点,任意三个点不在同一直线上,过任意三点作三角形,一共能作出多少不同的三角形?
(1)分析:当仅有3个点时,可作________个三角形;当有4个点时,可作________个三角形;当有5个点时,可作________个三角形;……
(2)归纳:考察点的个数n和可作出的三角形的个数Sn,发现:

(3)推理:________;
(4)结论:________.
查看答案和解析>>
科目: 来源:1+1轻巧夺冠·优化训练·八年级数学下 题型:059
(1)如图所示,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,过A作AG⊥EB,垂足为G,AG交BD于F,请说明OE=OF.

(2)对于上述命题,若点E在AC的延长线上,AG⊥EB交EB的延长线于点G,AG的延长线交DB的延长线于点F,其他条件不变,如下图所示,请你想一想,结论“OE=OF”还成立吗?如果成立,请给予说明;如果不成立,请说明理由.

查看答案和解析>>
科目: 来源:69领航·单元同步训练 八年级(上册) 数学(人教版) 题型:059
已知,△ABC是等边三角形,将一块含30°角的直角三角板DEF如图放置,让三角板在BC所在的直线上向右平移,当点E与点B重合时,点A恰好落在三角板的斜边DF上,问在三角板平移过程中,图中是否存在与线段EB始终相等的线段(假定AB,AC与三角板斜边的交点为G,H)?若存在,请指出这条线段,并证明,若不存在请说明理由.
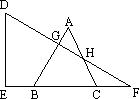
查看答案和解析>>
科目: 来源:萧红中学(四年制) 新概念数学 八年级上(人教版) 题型:059
| |||||||||||
查看答案和解析>>
科目: 来源:萧红中学(四年制) 新概念数学 八年级上(人教版) 题型:059
| |||||||||||
查看答案和解析>>
科目: 来源:学习周报 数学 北师大九年级版 2009-2010学年 第8期 总第164期 北师大版 题型:059
如图,△ABC是等腰直角三角形,D为斜边AB上的任意一点(不与点A、B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.
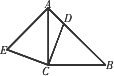
(1)求证:∠E+∠ADC=180°;
(2)猜想:当点D在何种特殊位置时,四边形AECD是何种特殊四边形?说明理由.
查看答案和解析>>
科目: 来源:学习周报 数学 北师大九年级版 2009-2010学年 第8期 总第164期 北师大版 题型:059
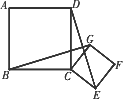
如图,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形.连接BG、DE.

(1)观察猜想BG与DE之间的大小关系,并证明你的结论;
(2)如图若把正方形CEFG绕点C旋转一个角度,(1)中你猜想的大小关系成立吗?若成立,证明你的结论;若不成立,说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com