若方程ax＋3=x－ay是关于x，y的二元一次方程，则a的取值范围是______．

已知方程是关于x、y的二元一次方程，则m=_______，n=_______．

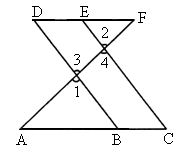
填理由，已知如图，E为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，求证：DF∥AC．

证明：∵∠1=∠2(已知)，∠1=∠3，∠2=∠4(　　)，∴∠3=∠4(等量代换)．

∴_____∥_______(　　)．

∴∠C=∠ABD(　　)

∵∠C=∠D(　　)，

∴∠D=∠ABD(　　)．

∴AC∥DF(　　)．

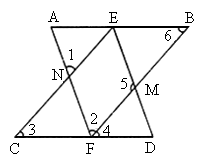
如图，(1)因为∠1=∠2，所以________∥_______．

(2)因为AB∥CD，所以∠4=_________．

(3)因为AF∥ED，所以∠AFD与_______互补．

如图所示，已知AB∥FD，ED∥AC，D是BC上一点，求证：∠A＋∠B＋∠C=180°．

证明：∵ED∥AC(①)，

∴∠A=②(③)，∠C=④(⑤)

∵AB∥FD(⑥)，

∴∠B=⑦(⑧)，∠4=∠2(⑨)

∵D是BC上一点(⑩)，

∴∠1＋∠2＋∠3=180°(⑾)

∴∠A＋∠B＋∠C=180°(⑿)

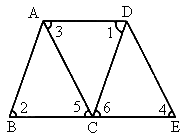
如图所示，AD∥BC，AC∥DE，∠1=∠2，可推出(1)∠3=∠4；(2)AB∥CD，试把理由填在括号内：

(1)∵AD∥BC(①)，

∴∠3=∠5(②)．

∵AC∥DE(③)，∴∠4=∠5(④)．

∴∠3=∠4(⑤)．

(2)∵AD∥BC(⑥)，

∴∠1=∠6(⑦)．

∵∠1=∠2(⑧)，∴∠2=∠6(⑨)．

∴AB∥CD(⑩)．

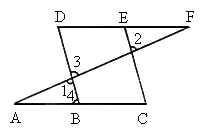
如图所示，∠1=∠2，∠A=∠F根据条件填空：

∵∠1=∠2(　　)，∠1=∠3(　　)，

∴∠2=∠3(　　)，∴CE∥BD(　　)．

∴∠4=∠C(　　)．∵∠1=∠2(　　)，

∴AC∥DF(　　)，∴∠4=∠D(　　)．

∴∠C=∠D(　　)．

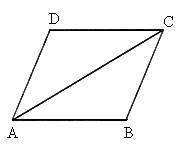
如图所示，①当______∥______时，∠BAC=∠DCA．

②当______∥______时，∠ADC＋∠DAB=180°．

③当______∥______时，AD∥BC．

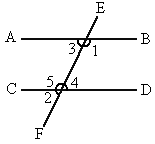
如图，直线AB、CD被直线EF所截，∠1＋∠2=180°．

求证：AB∥CD．

下面是证明过程，根据推理，填写理由．

证法1：∵直线CD与EF相交，

∴∠2=∠4(对顶角相等)．

∵∠1＋∠2=180°(　　　)，

∴∠1＋∠4=180°(　　　)．

∴AB∥CD(　　　)．

证法2：∵EF是直线(　　　)，

∴∠2＋∠5=180°(　　　)．

又∵∠1＋∠2=180°(　　　)，

∴∠1=∠5(　　　)．

∴AB∥CD(　　　)．

证法3：∵AB是直线(　　　)，

∴∠1＋∠3=180°(　　　)．

又∵∠1＋∠2=180°(　　　)，

∴∠2=∠3(　　　)．

∴AB∥CD(　　　)．

如图，完成下列推理，并在括号中写出相应的根据．

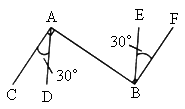
∵AC⊥AB，BF⊥AB(已知)，

∴∠CAB=∠ABF=90°(　　　　)．

∵∠CAD=∠EBF=30°(已知)，

∴_______=_______(　　　　)．

∴_______=_______(　　　　)．