上数学课时，陈老师让同学们解一道关于x、y的方程组并请小方和小龙两位同学到黑板上板演．可是小方同学看错了方程(1)中的a，得到方程组的解为小龙同学看错了方程(2)中的b，得到方程组的解为你能按正确的a、b值求出方程组的解吗？请试一试．

下列是按一定的规律排列的方程组和它的解的解集的对应关系图，若方程组集合中的方程组自左向右依次记作方程组1，方程组2，方程组3，…，方程组n．

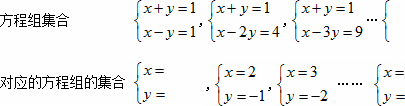
(1)将方程组1的解填入图中；

(2)请依据方程组和它的解的变化规律，将方程组n和它的解直接填入集合图中(注意：1－n²＝(1＋n)(1－n)；

(3)若方程组的解是求m的值，并判断该方程组是否符合题中的规律．

下表反映了按一定规律排列的方程组和它们的解的对应关系：

(1)写出方程组1的求解过程；

(2)请依据方程组和它们的解的变化规律，直接写出方程组n和它的解．(n为正整数)

张老师在一次“探究性学习”课中，设计了如下数表：

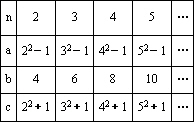
(1)请你分别观察a、b、c与n之间的关系，并用含自然数n(n＞1)的代数式表示a，b，c．

(2)猜想：以a、b、c为边的三角形是否为直角三角形？请证明你的猜想．

在△ABC中，a＝m²＋n²，b＝m²－n²，c＝2mn，且m＞n＞0，

(1)你能判断△ABC的最长边吗？请说明理由；

(2)△ABC是什么三角形，请通过计算的方法说明．

如图，是用硬纸板做成的两种直角三角形各有若干个，图①中两直角边长分别为a和b，斜边长为c；图②中两直角边长为C．请你动脑，将它们拼成能够证明勾股定理的图形．

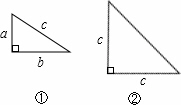
(1)请你画出一种图形，并验证勾股定理．

(2)你非常聪明，能再拼出另外一种能证明勾股定理的图形吗？请画出拼后的图形(无需证明)．

在教材中，我们通过数格子的方法发现了直角三角形的三边关系，利用四个完全相同的直角三角形拼图的方式验证了勾股定理的正确性．

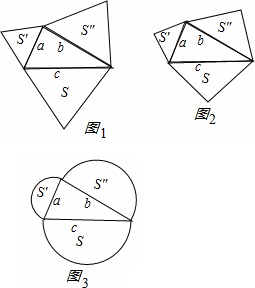
问题1：以直角三角形的三边为边向外作等边三角形，探究与S的关系(图1)．

问题2：以直角三角形的三边为斜边向外作等腰直角三角形，探究与S的关系(图2)．

问题3：以直角三角形的三边为直径向外作半圆，探究与S的关系(图3)．

已知Rt△ABC中，∠ACB＝90°，CA＝CB，有一个圆心角为45°，半径长等于CA的扇形CEF绕点C旋转，直线CE、CF分别与直线AB交于点M、N．

(1)如图①，当AM＝BN时，将△ACM沿CM折叠，点A落在弧EF的中点P处，再将△BCN沿CN折叠，点B也恰好落在点P处，此时，PM＝AM，PN＝BN，△PMN的形状是________等腰直角三角形．线段AM、BN、MN之间的数量关系是________MN)；

(2)如图②，当扇形CEF绕点C在∠ACB内部旋转时，线段MN、AM、BN之间的数量关系是________AM²＋BN²＝MN²．试证明你的猜想；

(3)当扇形CEF绕点C旋转至图③的位置时，线段MN、AM、BN之间的数量关系是________AM²＋BN²＝MN²．(不要求证明)

如图，EF是正方形两对边中点的连线段，将∠A沿DK折叠，使它的顶点A落在EF上的G点，求∠DKG的度数．

你知道吗？我们赖以生存的美丽的地球是一个近似于圆形的球体，它的半径长约1.496×10⁸千米．如果让你做一次旅行，沿着轨道乘飞船飞20天走完等于地球半径长的路程．请你计算一下，平均每天要飞行多少千米呢？(结果用科学记数法表示)．