若a＞0，b＜0，且|a|＜|b|，试比较a＋b，－a＋b，a－b，－a－b的值．

用一个平面去截一个正方体，截面可能是下面(下图)的图形吗？

降低文盲率，提高全民素质一向是我国发展大计中的重中之重．下表是我国历次人口普查中，每十万人中拥有的各种受教育程度人数的统计表：

为了表示近四十年来我国人口受教育程度的变化，一位同学制作了如下的统计图：

你认为他制作的统计图能直观反映出题目的意图吗？如果你觉得不合适，请你绘制出你认为最合适的统计图．

小明家有一根长15cm的玉笛，想放在长、宽、高分别为12cm、3cm、4cm的长方体盒子里保藏，你认为能放进去吗？为什么？

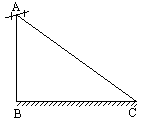
如图，有一根高为16米的电线杆BC在A处断裂，电线杆顶部C落在地面离电线杆底部B点8米远的地方，求电线杆的断裂处A离地面的距离．

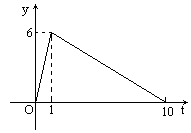
某医药研究所开发了一种新药，在试验药效时发现如果成人按规定剂量服用，那么服药后2小时时血液中含药量最高，达到每毫升6微克(1微克＝10^－3毫克)，接着逐步衰减，10小时时血液中含药量为每毫升3微克．每毫升血液中的含药量y(微克)随服药后的时间x(时)的变化如图所示．

(1)分别求出x≤2和x≥2时，y与x之间的函数关系式及自变量的取值范围；

(2)如果每毫升血液中含药量不少于4微克时在治疗疾病中是有效的，那么服药后经过多长时间开始有效？这个有效时间是多长？

某水产品养殖加工厂有200名工人，每名工人每天平均捕捞水产品50千克，或将当日所捕捞的水产品40千克进行精加工．已知每千克水产品直接出售可获利润6元，精加工后再出售，可获利润18元．设每天安排x名工人进行水产品精加工．

(1)求每天做水产品精加工所得利润y(元)与x的函数关系式；

(2)如果每天精加工的水产品和未来得及精加工的水产品全部出售，那么如何安排生产可使一天所获利润最大？最大利润是多少？

工厂生产某种产品，每件产品的出厂价为1万元，其原材料成本价(含设备损耗等)为0.55万元，同时在生产过程中平均每生产一件产品有1吨废渣产生，为达到国家环保要求，需要对废渣进行脱硫脱氮等处理，现有两种方案可供选择：

　　方案一：由工厂对废渣直接进行处理，每处理1吨废渣所用的原料为0.05万元，并且每月设备维护及损耗费为20万元，

　　方案二：工厂将废渣集中到废渣处理厂统一处理，每处理1吨需付0.1万元的处理费．

(1)设工厂每月生产x件产品，每月利润为y万元，分别求出方案一和方案二处理废渣时，y与x之间的函数关系式．(利润＝总收入－总支出)

(2)若你作为工厂负责人，如何根据月生产量选择处理方案，既可达到环保要求又最合算．

某公司到果园基地购买某种优质水果，慰问义务工作者，果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案．方案甲：每千克9元，由基地送货上门；方案乙：每千克8元，由顾客自己租车运回．已知从该公司租车到基地公司的运输费为5000元．

(1)分别写出该公司两种购买方案的总费用y(元)与所购买的水果量x(千克)之间的函数关系式，并写出自变量x的取值范围．

(2)当购买量在什么范围时，选择哪种购买方案付款最少？并说明理由．

在全国抗击“非典”的斗争中，黄冈研究所的医学专家们经过日夜奋战，终于研制出一种治疗非典型肺炎的抗生素．据临床观察：如果成人按规定的剂量注射这种抗生素，注射药液后每毫升血液中的含药量y(微克)与时间t(时)之间的函数关系近似地满足图中所示的折线．

(1)写出注射药液后每毫升血液中含药量y与时间t之间的函数关系式及自变量的取值范围．

(2)根据临床观察：每毫升血液中含药量不少于4微克时，控制“非典”病情是有效的．如果病人按规定的剂量注射该药液后，经过多长时间开始有效控制病情？这个有效时间有多长？

(3)假若某病人一天中第一次注射药液是早晨6点钟，问怎样安排此人从6∶00～20∶00注射药液的时间，才能使病人的治疗效果最好？