某工厂现有甲种原料360kg，乙种原料290kg，计划利用这两种原料生产A、B两种产品共50件，已知生产一件A种产品需用甲种原料9kg，乙种原料3kg，可获利润700元；生产一件B种产品需用甲种原料4kg，乙种原料10kg，可获利润1200元．

(1)按要求安排A、B两种产品的生产件数，有哪几种方案？请你设计出来．

(2)哪种方案利润最高？

有一个两位数，十位上的数字比个位上的数字大3，把个位数字与十位数字对调之后所得的新数与原数之和介于55和99之间，求这个两位数．

小华看着电视里的舞蹈节目：七个身穿不同民族服装的舞蹈演员正在面对观众进行队列变换，他陷入了沉思：这7个演员面对观众一共会有几种队列变换呢？……为了解决这一问题，他是这样思考和探索的：

①若只有一个演员A，那就只有队列变换A，共1种；

②若有两个演员A、B，那就有队列变换：AB和BA，共2种；

③若有三个演员A、B、C，那就有队列变换：ABC、ACB、BAC、BCA、CAB、CBA，共6种；

④若有四个演员A、B、C、D，那就有队列变换(小华把这四个字母在纸上不停的变换顺序地排列着、写着……数数看，哇！)有24种，变化如此之快呀．如有五个、六个、七个演员呢？看来不可一一的写下来数，还是找些规律吧，否则就……，还是智取吧……

列个表格试试看，记得书上有这样的例子，老师也曾示范过，它能更加清楚地反映其中的数字规律呢：

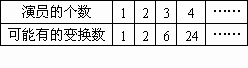
(1)你知道这7个舞蹈演员面对观众时一共有几种队列变换吗？说说你的想法．

(2)请你先仔细体会小华的解题策略，然后再探索：2²⁰的末位数字是多少？说说你是怎样想的．

观察下列等式9－1＝8　16－4＝12　25－9＝16　36－16＝20这些等式反映自然数间的某种规律，设n(n≥1)表示自然数，用关于n的等式表示这个规律．

若100(a－b)²＋(2k＋4)(b²－a²)＋400(a＋b)²是完全平方式，求k的值．

已知x³＋x²＋x＋1＝0，求1＋x＋x²＋x³＋…＋x²⁰⁰⁰的值．

观察下列各式：15²＝225；25²＝625；35²＝1225；…；个位数字是5的两位数平方后，末尾的两个数有什么规律？为什么？

　　有些自然数可以写成两个平方数(整数的平方)的和，例如：5＝1²＋2²，13＝2²＋3²，10＝1²＋3²，等等．

　　有趣的是这些数的积也可以写成两个平方数的和，例如5×13＝65＝1²＋8²＝4²＋7²，5×10＝50＝1²＋7²＝5²＋5²，等等．

　　一般地，两个平方和a²＋b²与c²＋d²的积一定也是这种形式的平方和，为什么呢？

　　道理很简单：我们做乘法(a²＋b²)(c²＋d²)＝a²c²＋a²d²＋b²c²＋b²d²…①然后将上式右边加上2abcd，再减去2abcd，变为a²c²＋2abcd＋b²d²＋a²d²－2abcd＋b²c²＝(ac＋bd)²＋(ad－bc)²，所以(a²＋b²)(c²＋d²)＝(ac＋bd)²＋(ad－bc)²．

　　例如(1²＋2²)(2²＋3²)＝(1×2＋2×3)²＋(1×3－2×2)²，这就是上面的5×13＝1²＋8²，在①式右边加上2abcd，再减去2abcd是为了配成完全平方，这种“配方法”是很有用的．

请用类似方法将130写成两个平方数的和．

已知a²＋b²＋4a－6b＋13＝0．求a、b的值．

(1－)(1－)(1－)…(1－)．