某工厂甲、乙两车间去年计划共完成税利720万元，结果甲车间完成计划的115％，乙车间完成了计划的110％，两车间共完成税利812万元，求去年这两个车间各超额完成税利多少万元？

用两个全等的等边三角形ABC和ACD拼成菱形ABCD．把一个含60°角的三角尺与这个菱形叠合，使三角尺60°角的顶点与点A重合，两边分别与AB，AC重合，将三角尺绕点A按逆时针方向旋转．

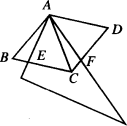
(1)当三角尺的两边分别与菱形的两边BC，CD相交于点E，F时(如图)，通过观察或测量BE，CF的长度，你能得出什么结论？证明你的结论．

(2)当三角尺的两边分别与菱形的两边BC，CD的延长线相交于点E，F时，你在(1)中得到的结论还成立吗？请自行画示意图，并简单说明理由．

求值：

(1)已知xy＝1，，求的值；

(2)已知，求式子的值．

某市的A县和B县春季育苗，急需化肥分别为90吨和60吨．该市的C县和D县分别储存化肥100吨和50吨，全部调配给A县和B县．已知C、D两县运化肥到A、B两县的运费(元/吨)如下表所示：

(1)设C县运到A县的化肥为x吨，求总运费ω(元)与x(吨)的函数关系式，并写出自变量x的取值范围；

(2)求最低总运费，并说明总运费最低时的运送方案．

如图表示甲、乙两名选手在一次自行越野赛中，路程y(千米)随时间x(分)变化的图象(全程)．根据图象回答下列问题：

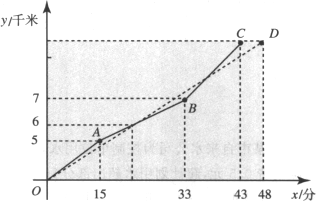
(1)求比赛开始多少分钟时，两人第一次相遇；

(2)求这次比赛全程是多少千米；

(3)求比赛开始多少分钟时，两人第二次相遇．

某市自来水公司为控制单位用水，每月只给某单位计划内用水3 000吨．计划内用水每吨收费0.5元，超计划用水超出部分每吨收费0.8元．如果单位自建水泵房抽水，每月需交500元管理费，另外每用一吨水再交0.28元．已知每抽一吨水需成本0.07元，问某单位每月用水超过3 000吨，该单位是用自来水公司的水合算还是自建水泵房抽水合算？

某货车租赁公司共有50辆货车，其中甲型20辆，乙型30辆．现将这50辆货车派往A、B两地，其中30辆派往A地，20辆派往B地．两地与该租赁公司商定的每天租赁价格见下表：

(1)设派往A地区为x辆乙型货车，租赁公司这50台货车一天获得的租金为y元，请写出y与x之间的函数关系式，并写出x的取值范围；

(2)若使租赁公司这50辆货车一天的租金不低于79 600元，则有多少种分派方案？请将各种方案设计出来；

(3)如果要使这50辆货车每天的租金最高，请你为该租赁公司提出一条合理建议．

某医药研究所开发了一种新药，如果成人按规定剂量服用，那么服药后每毫升血液中含药量y(微克)随时间x(小时)变化如图所示：

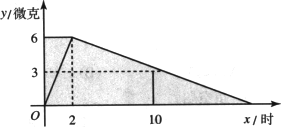
(1)分别求出x≤2和x≥2时，y与x之间函数关系式；

(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的，那么这个有效时间是多长？

某校20名同学去工厂进行寒假实践活动，每人每天可加工甲种零件5个或乙种零件4个．在这20名同学中派x人加工甲种零件，其余的加工乙种零件．已知每加工一个甲种零件可获利16元，每加工一个乙种零件可获利24元．

(1)写出此车间每天获利y(元)和x(人)之间的函数关系式；

(2)若要使车间每天获利不低于1 800元，问至少要派多少人加工乙种零件？

已知9＋与9－的小数部分分别是a和b，求a＋b的值．