如图所示，阴影图形绕着直线l旋转能形成怎样的几何体？将此问题与你的同伴探讨一下，可以动手试一试，再开动脑筋思考．

解方程＝0．

托尔斯泰是俄国著名的文学家，他一生喜欢有趣而又不太难的数学问题．下面这道题是托尔斯泰曾解过的题．

题目　　割草队要收割两块草地，其中一块比另一块大一倍，全队在大草地上收割半天之后，便一分为二，一半人继续留在大块草地上，另一半人转移到小块草地上，大块草地上留下的这一半人，到晚上就把大草地全部割完了；而小草地还剩一小块未割．第二天，这剩下的一小块，一个人花了一整天时间才割完，问：割草队中共有几个人？

托尔斯泰的解法：

既然在大块草地上割草队全体割了半天，全队的一半人又割了半天，那就很清楚，这一半人在半天时间内收割了大块草地的．因此，在小草地上，半队人割半天后剩下的草地为．根据题设，这剩下的，一个人一天割完，而在这之前全体人员一天总共割的草地为(即8个)．故割草队总人数等于8．

托尔斯泰特别对这道题可以用图解法求解感到满意(如图)，下面我们给出这道题的代数解法：

设x为割草队的人数，y表示每人每天所割草的面积(注意：y是辅助未知量，为列式方便而引入)，则每人半天所割草的面积为，全体人员半天所割草的面积为，半队人员半天所割草的面积为．所以，大块草地的面积为＋，小块草地的面积应为＋y．根据题设，大块草地面积为小块草地面积的两倍，可得方程

＋＝2(＋y)

即，＝2

约去y后，得＝2，解得x＝8

答：割草队的总人数为8人．

请结合你熟悉的生活、生产、科技等实际，编一道用不等式或不等式组知识解决的应用问题，并做出解答．

有一系列等式：

1×2×3×4＋1＝5²＝(1²＋3×1＋1)²，

2×3×4×5＋1＝11²＝(2²＋3×2＋1)²，

3×4×5×6＋1＝19²＝(3²＋3×3＋1)²，

4×5×6×7＋1＝29²＝(4²＋3×4＋1)²，

…

(1)根据你的观察、归纳、发现的规律，写出8×9×10×11＋1的结果；

(2)试猜想：n(n＋1)(n＋2)(n＋3)＋1是哪一个数的平方，并予以证明．

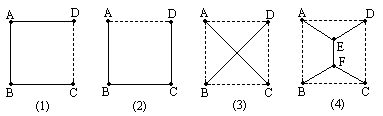
国家电力总公司为了改善农村用电电费过高的现状，目前正在全国各地农村进行电网改造．莲花村六组有四个村庄A、B、C、D正好位于一个正方形的四个顶点，现计划在四个村庄联合架设一条线路，他们设计了四种架设方案，如图中的实线部分，其中图(4)中，∠DAE＝∠ADE＝∠CBF＝∠BCF＝．请你帮助计算一下，哪种假设方案最省电线？(以下数据可供参考：＝1.414，＝1.732，＝2.236)

请同学们判断下列各式是否成立：

(1)＝2；(2)＝3；(3)＝4；(4)＝3．

经过计算可知，(1)、(2)、(3)式是成立的；(4)式是不成立的．这说明在二次根式的化简运算中要特别注意，根号里面的数是不能轻易地放到根号外面来的．

细心的同学可能会想，什么情况下根号里面的数能放到根号外面来呢？(1)、(2)、(3)式的成立仅仅是巧合吗？其中会有什么规律吧？我们来分析一下前三个式子的运算过程：

(1)＝＝＝2；

(2)＝＝＝3；

(3)＝＝＝4．

通过把带分数化成假分数的分数运算和分子开方运算验证了这些式子是成立的．

我们再来观察前三个等式左边根号内分数的特点．在三个带分数2、3、4中：

(1)整数部分与分数部分的分子相等：

2＝2，3＝3，4＝4；

(2)整数部分与分数部分的分母有下列关系：

3＝2²－1，8＝3²－1，15＝4²－1．

根据上面的分析和观察，我们不妨观察5＋＝5，式子＝5是不是也成立？

＝＝＝5

确实是成立的！

大胆地猜想一下，对于一般的形式a＋(a为大于1的整数)，式子

＝a

还会成立吗？我们来验证一下：

＝＝

＝＝a

(a为大于1的整数)．

太妙啦！我们的猜想是正确的．

那么，下列各式成立吗？

(1)＝2；(2)＝3；(3)＝4；(4)＝3．

能不能由此得出下面的结论呢？

＝a

同学们可能还会不满足，还会有更大胆的猜想！那就试试看吧．不要忘记，猜想成为真理，是要经过严格证明的．