阅读下面材料，再回答问题：

一般地，如果函数x＝f(x)对于自变量取值范围的的任意x，都有f(－x)＝－f(x)，那么y＝f(x)就叫做奇函数；如果y＝f(x)对于自变量取值范围内的任意x，都有f(－x)＝f(x)，那么y＝f(x)就叫做偶函数．

例如：f(x)＝x³＋x，当x取任意实数时，f(－x)＝(－x)³＋(－x)＝－x³－x＝－(x³＋x)，即f(－x)＝－f(x)，因此f(x)＝x³＋x为奇偶数．

又如f(x)＝|x|，当x取任意实数时，f(－x)＝|－x|＝|x|＝f(x)，即f(－x)＝f(x)，因此f(x)＝|x|是偶函数．

问题(1)：下列函数中：①y＝x⁴；②y＝x²＋1；③y＝；④y＝；⑤y＝x＋．奇函数有________，偶函数有________(只填序号)．

问题(2)：请你再分别写出一个奇函数、一个偶函数．

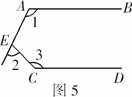
如图，已知AB∥CD，探究∠1，∠2，∠3之间的关系，并写出证明过程．

(1)如图①∠1＋∠2与∠B＋∠C有什么关系？为什么？

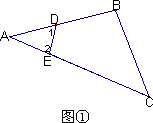
(2)把图①△ABC沿DE折叠，得到图②，填空：∠1＋∠2________∠B＋∠C(填“＞”“＜”“＝”)，当∠A＝40°时，∠B＋∠C＋∠1＋∠2＝________．

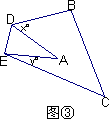
(3)如图③，是由图①的△ABC沿DE折叠得到的，如果∠A＝30°，则x＋y＝360°－(∠B＋∠C＋∠1＋∠2)＝360°－________＝________，猜想∠BDA＋∠CEA与∠A的关系为________．

在研究三角形内角和等于180°的证明方法时，小明和小虎分别给出了下列证法．

小明：在△ABC中，延长BC到D，

∴∠ACD＝∠A＋∠B(三角形一个外角等于和它不相邻的两个内角的和)．

又∵∠ACD＋∠ACB＝180°(平角定义)，

∴∠A＋∠B＋∠ACB＝180°(等式的性质)．

小虎：在△ABC中，作CD⊥AB(如图)，

∵CD⊥AB(已知)，

∴∠ADC＝∠BDC＝90°(直角定义)．

∴∠A＋∠ACD＝90°，∠B＋∠BCD＝90°(直角三角形两锐角互余)．

∴∠A＋∠ACD＋∠B＋∠BCD＝180°(等式的性质)．

∴∠A＋∠B＋∠ACB＝180°．

请你判断上述两名同学的证法是否正确，如果不正确，写出一种你认为较简单的证明三角形内角和定理的方法，与同伴交流．

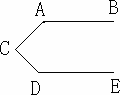
如图，已知AB∥DE，试求证：∠A＋∠ACD＋∠D＝360⁰(你有几种证法？)

已知△ABC的高为AD，∠BAD＝70o，∠CAD＝20o，求∠BAC的度数．

如图所示，已知∠xOy＝90°，点A，B分别在射线Ox，Oy上移动，BE是∠ABy的平分线，BE的反向延长线与∠OAB的平分线交于点C，试问∠ACB的大小是否发生变化？

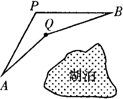
湖边上有A，B两个村庄(如图)，从A到B有两条路可走，即A→P→B和A→Q→B．试判别哪条路更短，并说明理由．

已知△ABC中，三边长a，b，c都是整数，且满足a＞b＞c，a＝8，那么满足条件的三角形共有多少个？

一块模板如图所示，按规定AF与DE的延长线相交成70°，但交点不在模板上，不便测量，于是王师傅连接AD，测得∠FAD＝34°，∠ADE＝76°，请你根据这两个角度判断模板是否合格？并说明理由．