
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如下图所示,已知A为∠POQ的边OQ上一点,以A为顶点的∠MAN的两边分别交射线OP于M,N两点,且∠MAN=∠POQ=α(α为锐角).当∠MAN以点A为旋转中心,AM边从与AO重合的位置开始,按逆时针方向旋转(∠MAN保持不变)时,M,N两点在射线OP上同时以不同的速度向右平移.设OM=x,ON=y(y>x≥0),△AOM的面积为S,且cosα,OA是方程2z2-5z+2=0的两个根.
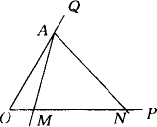
(1)当∠MAN旋转30°(即∠OAM=30°)时,求点N移动的距离;
(2)求证AN2=ON·MN;
(3)试求y与x之间的函数关系式及自变量x的取值范围;
(4)试写出S随x变化的函数关系式,并确定S的取值范围.
查看答案和解析>>
科目: 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:044
如图所示是某一公路路基的设计简图,等腰梯形ABCD表示它的横断面,原计划设计的坡角为![]() ,坡长AD=6.5 m,现考虑短期内车流量会增加,需增加路面宽度,故改变设计方案,将图中(一)、(二)两块分别补到上部(三)、(四)的位置,使横断面EFGH为等腰梯形,重新设计后路基的坡角为
,坡长AD=6.5 m,现考虑短期内车流量会增加,需增加路面宽度,故改变设计方案,将图中(一)、(二)两块分别补到上部(三)、(四)的位置,使横断面EFGH为等腰梯形,重新设计后路基的坡角为![]() ,全部工程的土方数不变,问重新设计后,路面宽将增加多少?(精确到0.1 m)
,全部工程的土方数不变,问重新设计后,路面宽将增加多少?(精确到0.1 m)

查看答案和解析>>
科目: 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:044
| |||||||||||
查看答案和解析>>
科目: 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:044
某家具加工厂的木板余料是如图所示的四边形ABCD,已知∠B=∠D=![]() ,∠C=
,∠C=![]() ,AD=20 cm,BC=40 cm.家具厂要从这种木板余料中截出两种不同规格的矩形木板,要求截出的矩形木板的面积尽可能地大,你能帮助家具厂设计切割方案并求出截得的矩形木板的面积吗?
,AD=20 cm,BC=40 cm.家具厂要从这种木板余料中截出两种不同规格的矩形木板,要求截出的矩形木板的面积尽可能地大,你能帮助家具厂设计切割方案并求出截得的矩形木板的面积吗?
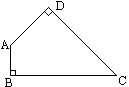
查看答案和解析>>
科目: 来源:广东省湛江市2011-2012学年八年级第四次月考数学试题 题型:044
A市和B市库存某种机器分别为12台和6台,现决定支援给C市10台和D市8台,已知从A市调运一台机器到C市和D市的运费分别为400元和800元,从B市调运一台机器到C市和D市的运费分别为300元和500元.
(1)设B市运往C市的机器x台,求总运费W(元)与x的函数式.
(2)若要求总运费不超过9000元,问:共有几种调运方案.
(3)请选择最佳调运方案,使总运费最少,并求出最少总运费.
查看答案和解析>>
科目: 来源:浙江省杭州市2011-2012学年七年级下学期期中考试数学试题 题型:044
如图a△ABC和△CEF是两个大小不等的等边三角形(等边三角形为三条边相等,三个角为60°的三角形)且有一个公共顶点C,点F、B、C在同一直线上,连结AF和BE.

(1)线段AF和BE有怎样的大小关系?(写出结论,不需要说明理由)
(2)将图a中的△CEF绕点C旋转一定的角度,得到图b,(1)中的结论还成立吗?作出判断并说明理由;
(3)若将图a中的△ABC绕点C旋转一定的角度,请你画出一个变换后的图形c(草图即可)(1)中的结论还成立吗?作出判断不必说明理由.
查看答案和解析>>
科目: 来源:北京市四中2011-2012学年八年级下学期期中考试数学试题 题型:044
如图1,将∠EAF绕着四边形ABCD的顶点A顺时针旋转,∠EAF的两边分别与DC的延长线交于点F,与CB的延长线交于点E,连接EF.
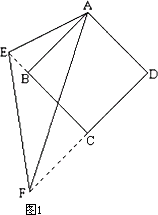
(1)若四边形ABCD为正方形,当∠EAF=45°时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
(2)如图2,如果四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAF=![]() ∠BAD时,EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式并给予证明.
∠BAD时,EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式并给予证明.
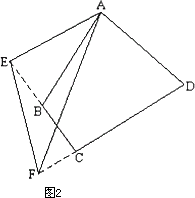
(3)在(2)中,若BC=4,DC=7,CF=2,求△CEF的周长(直接写出结果即可).
查看答案和解析>>
科目: 来源:江苏省无锡市崇安区2011-2012学年七年级下学期期中考试数学试题 题型:044
我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:如图1,在四边形ABCD中,取对角线BD的中点O,连结OA、OC.显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于E,则直线AE即为一条“好线”.
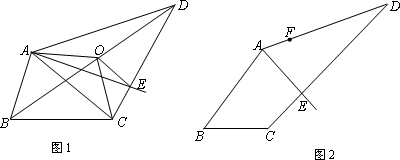
(1)试说明直线AE是“好线”的理由;
(2)如图2,AE为一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,只需对画图步骤作适当说明(不需要说明“好线”的理由).
查看答案和解析>>
科目: 来源:江苏省昆山市2011-2012学年七年级下学期期中考试数学试题 题型:044
探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
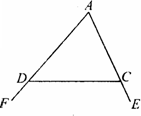
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
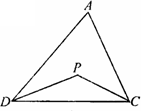
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
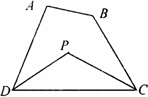
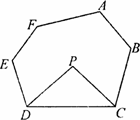
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:________.
查看答案和解析>>
科目: 来源:湖北省黄冈市2012届九年级2月中考摸底考试数学试题 题型:044
如图,在坐标系中,菱形ABCD的边BC与x轴重合,点B与原点重合,AB=10,∠ABC=60°.动点P从点B出发沿BC边以每秒1个单位长的速度匀速运动;动点Q从点D出发沿折线DC-CB-BA以每秒3个单位长的速度匀速运动,过点P作PF⊥BC,交折线AB-AC于点E,交直线AD于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之停止,设运动时间为t秒.
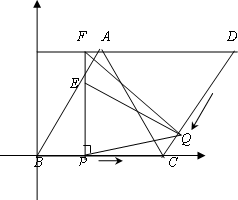
(1)写出点A与点D的坐标
(2)当t=3秒时,试判断QE与AB之间的位置关系?
(3)当Q在线段DC上运动时,若△PQF为等腰三角形,求t的值;
(4)设△PQE的面积为S,求S与t的函数关系式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com