
科目: 来源: 题型:044
如图1,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点P是对角线BD上的一点,PQ∥BA交AD于点Q,PS∥BC交DC于点S,四边形PQRS是平行四边形。
(1)当点P与点B重合时,图1变为图2,若∠ABD=90°,求证:△ABR≌△CRD;
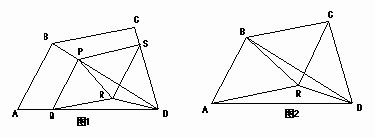
【证】
(2)对于图1,若四边形PRDS也是平行四边形,此时,你能推出四边形ABCD还应满足什么条件?
查看答案和解析>>
科目: 来源: 题型:044
如图,AD=BC,请添加一个条件,使图中存在全等三角形并给予证明.
你所添加的条件为: ;
得到的一对全等三角形是△______≌△______.
证明:

查看答案和解析>>
科目: 来源: 题型:044
如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC。
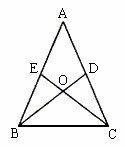
(1)上述四个条件中,哪两个条件可判定△ABC是等腰三角形:_____________,_____________。
(2)根据你所选的条件,证明△ABC是等腰三角形。
查看答案和解析>>
科目: 来源: 题型:044
如图,已知:梯形ABCD中,AD∥BC,E为AC的中点,连接DE并延长交BC于点F,连接AF.
(1)求证:AD=CF;
(2
)在原有条件不变的情况下,请你再添加一个条件(不再增添辅助线),使四边形AFCD成为菱形,并说明理由.![]()
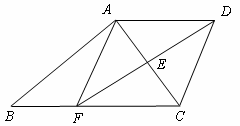
查看答案和解析>>
科目: 来源: 题型:044
如图:四边形ABCD中,E、F、G、H分别为各边的中点,顺次连结E、F、G、H,把四边形EFGH称为中点四边形。连结AC、BD,容易证明:中点四边形EFGH一定是平行四边形。
(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD的对角线满足AC=BD时,四边形EFGH为菱形;
当四边形ABCD的对角线满足_______________时,四边形EFGH为矩形;
当四边形ABCD的对角线满足________________时,四边形EFGH为正方形。
(2)探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系,请写出你发现的结论,并加以证明。
(3)如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是多少?
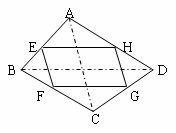
查看答案和解析>>
科目: 来源: 题型:044
如图所示,在![]() 中,
中,![]() 分别是
分别是![]() 和
和![]() 上的一点,
上的一点,![]() 与
与![]() 交于点
交于点![]() ,给出下列四个条件:①
,给出下列四个条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
(1
)上述四个条件中,哪两个条件可以判定(2
)选择(1)小题中的一种情形,证明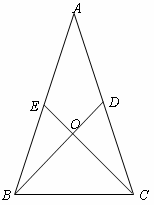
查看答案和解析>>
科目: 来源: 题型:044
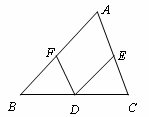
如图,在△![]() 中,
中,![]() 为
为![]() 边的中点,过
边的中点,过![]() 点分别作
点分别作![]() ∥
∥![]() 交
交![]() 于点
于点![]() ,
,![]() ∥
∥![]() 交
交![]() 于点
于点![]() .
.
(1)证明:△![]() ≌△
≌△![]() ;
;
(2)如果给△![]() 添加一个条件,使四边形
添加一个条件,使四边形![]() 成为菱形,则该条是 ;
成为菱形,则该条是 ;
如果给△![]() 添加一个条件,使四边形
添加一个条件,使四边形![]() 成为矩形,则该条件是 .
成为矩形,则该条件是 .
(均不再增添辅助线) 请选择一个结论进行证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com