
科目: 来源: 题型:044
如图l,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM![]() BE,垂足为M,AM交BD于点F.
BE,垂足为M,AM交BD于点F.
(1)
求证:OE=OF;(2)
如图2,若点E在AC的延长线上,AM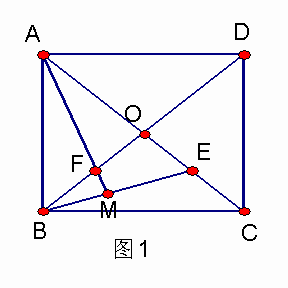

查看答案和解析>>
科目: 来源: 题型:044
△ABC中,BC=![]() ,AC=
,AC=![]() ,AB=c.若
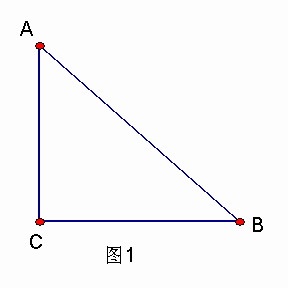
,AB=c.若![]() ,如图l,根据勾股定理,则
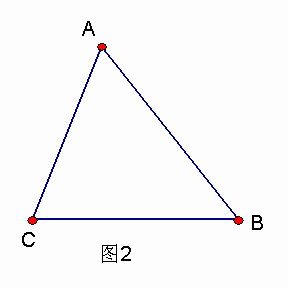
,如图l,根据勾股定理,则![]() 。若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想
。若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想![]() 与
与![]() 的关系,并证明你的结论.
的关系,并证明你的结论.

查看答案和解析>>
科目: 来源: 题型:044
下图的数阵是由全体奇数排成
(1
)图中平行四边形框内的九个数之和与中间的数有什么关系?(2
)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;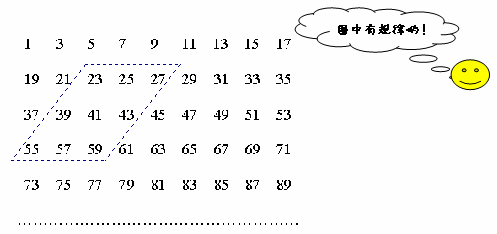
(3
)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个,若不能,请说出理由。查看答案和解析>>
科目: 来源: 题型:044
如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难证明S1=S2+S3 .
(1) 如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(不必证明)
(2) 如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明;
(3)
若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1、S2、S3表示,为使S1、S2、S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件?证明你的结论;(4)
类比(1)、(2)、(3)的结论,请你总结出一个更具一般意义的结论 .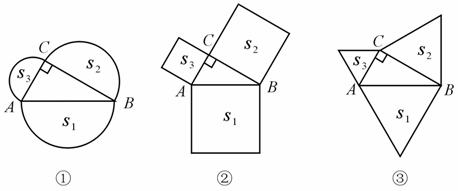
查看答案和解析>>
科目: 来源: 题型:044
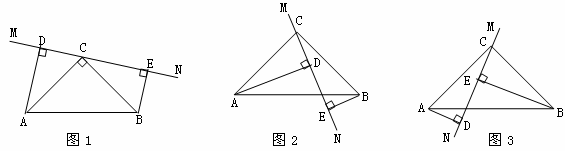
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
注意:第(2) 、(3)小题你选答的是第 小题.
查看答案和解析>>
科目: 来源: 题型:044
把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
(1)在上述旋转过程中,BH与CH有怎样的数量关系?四边形BHGK的面积有何变化?证明你发现的结论;
(2)连接HK,在上述旋转过程中,设BH=![]() ,△GKH的面积为
,△GKH的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)
在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的
查看答案和解析>>
科目: 来源: 题型:044
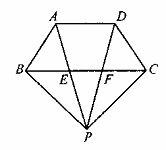
如图,梯形ABCD中,AD∥BC,AB=DC,P为梯形ABCD外一点,PA、PD分别交线段BC于点E、F,且PA=PD。
(1)写出图中三对你认为全等的三角形(不再添加辅助线);
(2)选择你在(1)中写出的全等三角形中的任意一对进行证明。
查看答案和解析>>
科目: 来源: 题型:044
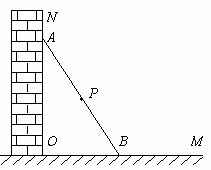
如图所示,一根长2a的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P. 若木棍A端沿墙下滑,且B端沿地面向右滑行.
(1)请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由.
(2)在木棍滑动的过程中,当滑动到什么位置时,△AOB的面积最大?简述理由,并求出面积的最大值.
查看答案和解析>>
科目: 来源: 题型:044
如图,有一块塑料矩形模板ABCD,长为10![]() ,宽为4
,宽为4![]() ,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A、D重合),在AD上适当移动三角板顶点P:
,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A、D重合),在AD上适当移动三角板顶点P:
①能否使你的三角板两直角边分别通过点B与点C ?若能,请你求出这时AP 的长;若不能,请说明理由.
②再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH始终通过点B,另一直角边PF与DC延长线交于点Q,与BC交于点E,能否使CE=2 ![]() ?若能,请你求出这时AP的长;若不能,请你说明理由.
?若能,请你求出这时AP的长;若不能,请你说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com