
科目: 来源: 题型:044
已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF。请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可)。
(1
)连结____________;(2
)猜想:______=______;(3
)证明: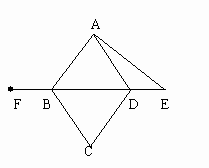
查看答案和解析>>
科目: 来源: 题型:044
如图,已知平行四边形![]() 及四边形外一直线
及四边形外一直线![]() ,四个顶点
,四个顶点![]()
![]()
![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() .
.
(1)观察图形,猜想得出![]() 满足怎样的关系式?证明你的结论.
满足怎样的关系式?证明你的结论.
(2)现将![]() 向上平移,你得到的结论还一定成立吗?请分情况写出你的结论.
向上平移,你得到的结论还一定成立吗?请分情况写出你的结论.

查看答案和解析>>
科目: 来源: 题型:044
如图1,已知△ABC的高AE=5,BC=![]() ,∠ABC=45°,F是AE上的点,G是点E关于F的对称点,过点G作BC的平行线与AB交于H、与AC交于I,连接IF并延长交BC于J,连接HF并延长交BC于K.
,∠ABC=45°,F是AE上的点,G是点E关于F的对称点,过点G作BC的平行线与AB交于H、与AC交于I,连接IF并延长交BC于J,连接HF并延长交BC于K.
(1
)请你探索并判断四边形HIKJ是怎样的四边形?并对你得到的结论予以证明;(2
)当点F在AE上运动并使点H、I、K、J都在△ABC的三条边上时,求线段AF长的取值范围.
(
图2供思考用)查看答案和解析>>
科目: 来源: 题型:044
如图,在矩形ABCD中,F是BC边上的一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC,根据上述条件,请你在图中找出一对全等三角形,并证明你的结论。
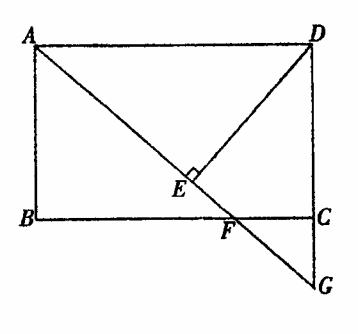
查看答案和解析>>
科目: 来源: 题型:044
如图1,操作:把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC),取线段AE的中点M。
探究:线段MD、MF的关系,并加以证明。
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);(2)在你经历说明(1)的过程之后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明。
注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分。
① DM的延长线交CE于点N,且AD=NE;
② 将正方形CGEF绕点C逆时针旋转45°(如图2),
其他条件不变;③在②的条件下且CF=2AD。
附加题:将正方形CGEF绕点C旋转任意角度后(如图3),其他条件不变。探究:线段MD、MF的关系,并加以证明。
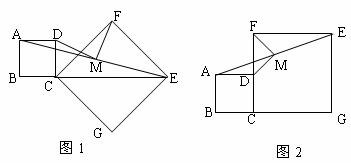

查看答案和解析>>
科目: 来源: 题型:044
已知任意四边形ABCD,且线段AB、BC、CD、DA、AC、BD的中点分别是E、F、G、H、P、Q.
(1)若四边形ABCD如图①,判断下列结论是否正确(正确的在括号里填摗虜,错误的在括号里填摗翑)
甲:顺次连接EF、FG、GH、HE一定是平行四边形;( )
乙:顺次连接EQ、QG、GP、PE一定得到平行四边形;( )
(2)请选择甲、乙中的一个,证明你对它的判断;
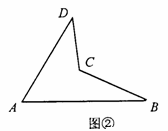
(3)若四边形ABCD如图②,请你判断(1)中的两个结论是否成立?
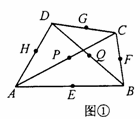
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com