
科目: 来源: 题型:044
[尝试]如图,把一个等腰直角△ABC沿斜边上的中线CD(裁剪线)剪一刀,把分割成的两部分拼成一个四边形A′BCD,如示意图(1).(以下有画图要求的,工具不限,不必写画法和证明)
(1)猜一猜:四边形A′BCD一定是__________;
(2)试一试:按上述的裁剪方法,请你拼一个与图(1)不同的四边形,并在图(2)中画出示意图.

[探究]在等腰直角△ABC中,请你沿一条中位线(裁剪线)剪一刀,把分割成的两部分拼成一个特殊四边形.
(1)想一想:你能拼得的特殊四边形分别是________________;(写出两种)
(2)画一画:请分别在图(3)、图(4)中画出你拼得的这两个特殊四边形的示意图.
[拓广]在等腰直角△ABC中,请你沿一条与中线、中位线不同的裁剪线剪一刀,把分割成的两部分拼成一个特殊四边形.
(1)变一变:你确定的裁剪线是________________,(写出一种)拼得的特殊四边形是______;
(2)拼一拼:请在图(5)中画出你拼得的这个特殊四边形的示意图.
查看答案和解析>>
科目: 来源:东城区2001~2002学年度第一学期教学目标检测·初三数学No.1~No.20 题型:044
若二次函数y=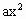 +bx+c的图象经过点(0,3),图象顶点坐标为(2,-1),求二次函数的解析式.
+bx+c的图象经过点(0,3),图象顶点坐标为(2,-1),求二次函数的解析式.
查看答案和解析>>
科目: 来源:东城区2001~2002学年度第一学期教学目标检测·初三数学No.1~No.20 题型:044
已知一次函数y=kx+b的图象经过点(3,0),且与坐标轴围成的三角形的面积为6,求这个一次函数的解析式.
查看答案和解析>>
科目: 来源: 题型:044
我们把分子为1的分数叫做单位分数. 如![]() ,
,![]() ,
,![]() …,任何一个单位分数都可以拆分成两个不同的单位分数的和,如
…,任何一个单位分数都可以拆分成两个不同的单位分数的和,如![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,…
,…
(1)根据对上述式子的观察,你会发现![]() . 请写出□,○所表示的数;
. 请写出□,○所表示的数;
(2)进一步思考,单位分数![]() (n是不小于2的正整数)
(n是不小于2的正整数)![]() ,请写出△,☆所表示的式,并加以验证.
,请写出△,☆所表示的式,并加以验证.
查看答案和解析>>
科目: 来源: 题型:044
如图:∠MON = 90°,在∠MON的内部有一个正方形AOCD,点A、C分别在射线OM、ON上,点B1是ON上的任意一点,在∠MON的内部作正方形AB1C1D1。
(1)连续D1D,求证:∠ADD1 = 90°;
(2)连结CC1,猜一猜,∠C1CN的度数是多少?并证明你的结论;
(3)在ON上再任取一点B2,以AB2为边,在∠MON的内部作正方形AB2C2D2,观察图形,并结合(1)、(2)的结论,请你再做出一个合理的判断。

查看答案和解析>>
科目: 来源: 题型:044
为保证交通安全,汽车驾驶员必须知道汽车刹车后的停止距离(开始刹车到车辆停止车辆行驶的距离)与汽车行驶速度(开始刹车时的速度)的关系,以便及时刹车.
下表是某款车在平坦道路上路况良好时刹车后的停止距离与汽车行驶速度的对应值表:

(1
)设汽车刹车后的停止距离(2
)根据你所选择的函数解析式,若汽车刹车后的停止距离为查看答案和解析>>
科目: 来源: 题型:044
如图,在梯形纸片ABCD中,AD∥BC,AD > CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C’E
(1
)求证:四边形CDC’E是菱形;(2
)若BC = CD + AD,试判断四边形ABED的形状,并加以证明.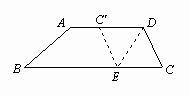
查看答案和解析>>
科目: 来源:东城区2001~2002学年度第一学期教学目标检测·初三数学No.1~No.20 题型:044
如图所示,公园要建造圆形的喷水地,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25m
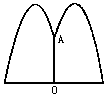
(1)如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?
(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流最大高度应达到多少米?(精确到0.1m)
(提示,可建立如下坐标系:以OA所在直线为y轴,过点O垂直于OA的直线为x轴,点O为原点)
查看答案和解析>>
科目: 来源:东城区2001~2002学年度第一学期教学目标检测·初三数学No.1~No.20 题型:044
A校和B校各有旧电脑12台和6台,现决定送给C校10台,D校8台,已知从A校调一台电脑到C校、D校的运费分别是40元和80元;从B校调运一台电脑到C校、D校的运费分别是30元和50元,试求出总运费最低的调运方案;最低运费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com