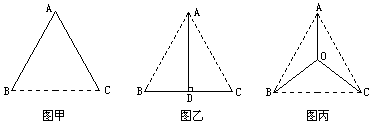
由于水资源缺乏，B、C两地不得不从黄河上的扬水站A处引水，这就需要在A、B、C之间铺设地下输水管道，有人设计了三种铺设方案：如图甲、乙、丙，图中实线表示管道铺设线路，在图乙中，AD⊥BC于D；在图丙中，OA＝OB＝OC．为减少渗漏，节约水资源，并降低工程造价，铺设线路应尽量缩短．已知△ABC恰好是一个边长为a的等边三角形，请你通过计算，判断哪个铺设方案最好．

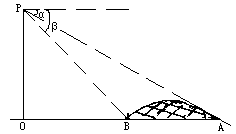
如图直升飞机在跨河大桥AB的上方P点处，此时飞机离地面的高度PO＝450m，且A、B、O三点在一条直线上，测得大桥两端的俯角分别为α=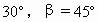，求大桥AB的长．(精确到1m)

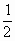已知△ABC中，∠C＝，边BC的长和∠A的余弦值分别是方程(x－)(x－3)＝0的两个实数根，求边AB的长．

为加强对洪灾的防御，某河流沿岸要修筑一条长2000米的防洪大坝，大坝的横断面如图所示，求修筑这条大坝所需的土方量是多少？(保留三个有效数字，＝1.732)

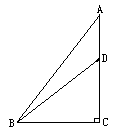
如图，在Rt△ABC中，∠C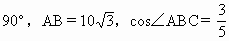＝，D为AC上一点，∠DBC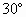＝，求AD的长．

已知：AD是△ABC中BC边上的高，∠BAD＝α，AD＝12cm，BC＝14cm，

tanα＝．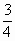　　

求(1)AB，AC的长；

(2)sinB·cosC的值．

求锐角α

已知α是锐角，cosα＝，求sinα，tanα，cotα的值．

操作：如图①，△ABC是正三角形，△BDC是顶角∠BDC＝120°的等腰三角形，以D为顶点作一个60°角，角的两边分别交AB、AC边于M、N两点，连接MN．

探究：线段BM、MN、NC之间的关系，并加以证明．

说明：⑴如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；⑵在你经历说明⑴的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明．

注意：选取①完成证明得10分；选取②完成证明得5分．

①（如图②）；　　②（如图③）．

附加题：若点M、N分别是射线AB、CA上的点，其它条件不变，再探线段BM、MN、NC之间的关系，在图④中画出图形，并说明理由．

如图，，，点在同一直线上，．

(1）求证：；

(2）连结，试猜想四边形是什么四边形，并证明你的结论．