
科目: 来源:东城区2001~2002学年度第一学期教学目标检测·初三数学No.1~No.20 题型:044
已知:如图,△ABC中,∠C=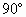 ,以BC为直径的⊙O交AB于D,过D点作⊙O的切线EF交AC于E.
,以BC为直径的⊙O交AB于D,过D点作⊙O的切线EF交AC于E.

(1)求证:DE=AE;
(2)若BC=3,DE=2,求AD的长.
查看答案和解析>>
科目: 来源:东城区2001~2002学年度第一学期教学目标检测·初三数学No.1~No.20 题型:044
已知:如图,在△ABC中,∠BAC=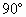 ,以AB为直径作⊙O交BC于D点,过D点作⊙O切线交AC于E.求证:AE=EC.
,以AB为直径作⊙O交BC于D点,过D点作⊙O切线交AC于E.求证:AE=EC.

查看答案和解析>>
科目: 来源:东城区2001~2002学年度第一学期教学目标检测·初三数学No.1~No.20 题型:044
已知:如图,AB是⊙O的直径.EF切⊙O于C,AD⊥EF于D,且AD=2,AB=6.求:AC的长.
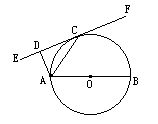
查看答案和解析>>
科目: 来源:东城区2001~2002学年度第一学期教学目标检测·初三数学No.1~No.20 题型:044
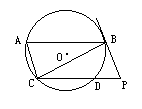
已知:如图,在⊙O中,弦AB∥CD.连AC,BC,过点B作⊙O的切线交CD的延长线于P.求证: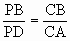 .
.
查看答案和解析>>
科目: 来源:东城区2001~2002学年度第一学期教学目标检测·初三数学No.1~No.20 题型:044
已知:如图,△CDF内接于⊙O,AB为⊙O的直径,且AB⊥CD,BE∥CD交FC的延长线于E.
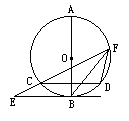
求证:(1)BE为⊙O的切线;
(2)BF2=FD·EF.
查看答案和解析>>
科目: 来源:东城区2001~2002学年度第一学期教学目标检测·初三数学No.1~No.20 题型:044
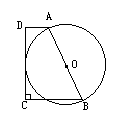
已知:如图,直角梯形ABCD中,AD∥BC,∠C=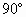 ,且AB=AD+BC.求证:以AB为直径的圆与CD相切.
,且AB=AD+BC.求证:以AB为直径的圆与CD相切.
查看答案和解析>>
科目: 来源:东城区2001~2002学年度第一学期教学目标检测·初三数学No.1~No.20 题型:044
已知:如图,△ABC内接于⊙O,MN过点A且∠NAC=∠ABC.求证:MN与⊙O相切.
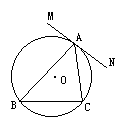
查看答案和解析>>
科目: 来源: 题型:044
已知:△ABC中,AB=10
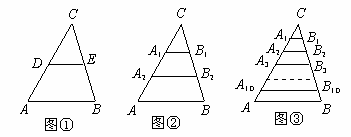
⑴如图①,若点D、E分别是AC、BC边的中点,求DE的长;
⑵如图②,若点A1、A2把AC边三等分,过A1、A2作AB边的平行线,分别交BC边于点B1、B2,求A1B1+A2B2的值;
⑶如图③,若点A1、A2、…、A10把AC边十一等分,过各点作AB边的平行线,分别交BC边于点B1、B2、…、B10。根据你所发现的规律,直接写出A1B1+A2B2+…+A10B10的结果。
查看答案和解析>>
科目: 来源: 题型:044
设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去···。
(1)记正方形ABCD的边长为![]() =1,依上述方法所作的正方形的边长依次为
=1,依上述方法所作的正方形的边长依次为![]() ,
,![]() ,
,![]() ,···,
,···,![]() ,求出
,求出![]() ,
,![]() ,
,![]() 的值。
的值。
(2
)根据以上规律写出第n个正方形的边长
查看答案和解析>>
科目: 来源: 题型:044
我们知道:由于圆是中心对称图形有,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1)。

探索下列问题:
(
1)在图2给出的四个正方形中,各画出一条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意直线),将每个正方形都分割成面积相等的两部分;
(2
)一条竖直方向的直线m以及任意直线n,在由左向右平移的过程中,将六边形分成左右两部分,其面积分别记为S1和S2。① 你在图3中相应图形下方的横线上分别填写S1与S2的数量关系式(用摚紨,摚綌,摚緮连接);

② 请你在图4中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用摚紨,摚綌,摚緮连接)。

(3
)是否存在一条直线,将一个任意平面图形(如图11-5)分割成面积相等的两部分?请简略说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com