
科目: 来源: 题型:044
老师在黑板上写出三个算式: 5![]() 一
3
一
3![]() = 8×2,9
= 8×2,9![]() -7
-7![]() =8×4,15
=8×4,15![]() -3
-3![]() =8×27,
=8×27,
王华接着又写了两个具有同样规律的算式:11![]()
![]() 5
5 ![]() =8×12,15
=8×12,15![]() -7
-7![]() =8×22,……
=8×22,……
(1)请你再写出两个(不同于上面算式)具有上述规律的算式;
(2)用文字写出反映上述算式的规律;
(3 )证明这个规律的正确性.
查看答案和解析>>
科目: 来源: 题型:044
第一象限内的点A在一反比例函数的图象上,过A作![]() 轴,垂足为B,连AO,已知
轴,垂足为B,连AO,已知![]() 的面积为4。
的面积为4。
(1)求反比例函数的解析式;
(2)若点A的纵坐标为4,过点A的直线与x轴交于P,且![]() 与
与![]() 相似,求所有符合条件的点P的坐标。
相似,求所有符合条件的点P的坐标。
(3)在(2)的条件下,过点P、O、A的抛物线是否可由抛物线![]() 平移得到?若是,请说明由抛物线
平移得到?若是,请说明由抛物线![]() 如何平移得到;若不是,请说明理由。
如何平移得到;若不是,请说明理由。
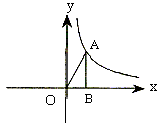
查看答案和解析>>
科目: 来源:黄冈重点作业 初三数学(下) 题型:044
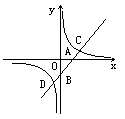
如图所示,一次函数的图像与x轴、y轴分别交于A、B两点,与反比例函数的图像交于C、D两点.如果点A的坐标为(2,0),点C、D分别在第一、三象限,且OA=OB=AC=BD.试求一次函数和反比例函数的解析式.
查看答案和解析>>
科目: 来源: 题型:044
某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元进行批量生产.已知生产每件产品的成本为40元, 在销售过程中发现,当销售单价定为100元时,年销售时为20万件;销售单价每增加10元, 年销售量将减少1万件.设第一年销售单价为x元,销售量为y万件,获利(年获利=年销售额-生产成本-投资)为z万元.
(1)试写出y与x之间的函数关系式;(不必写出x的取值范围)
(2)试写出z与x之间的函数关系式;(不必写出x的取值范围)
(3)计算销售单价为160元时的获利,并说明同样的获利,销售单价还可以定为多少元?相应的销售量分别为多少万件?
查看答案和解析>>
科目: 来源: 题型:044
善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间![]() (单位:分钟)与学习收益量
(单位:分钟)与学习收益量![]() 的关系如图1所示,用于回顾反思的时间
的关系如图1所示,用于回顾反思的时间![]() (单位:分钟)与学习收益
(单位:分钟)与学习收益![]() 的关系如图2所示(其中
的关系如图2所示(其中![]() 是抛物线的一部分,
是抛物线的一部分,![]() 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1
)求小迪解题的学习收益量(2
)求小迪回顾反思的学习收益量(3
)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?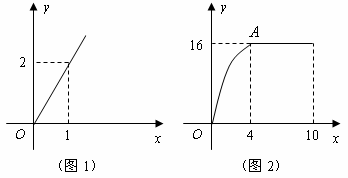
查看答案和解析>>
科目: 来源:黄冈重点作业 初三数学(下) 题型:044
已知二次函数y=x2+bx+c(b,c为常数).
(1)若二次函数的图像经过A(-2,-3)和B(2,5)两点,求此二次函数的解析式;
(2)若(1)中的二次函数的图像过点P(m+1,n2+4n),且m≠n,求m+n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com