
科目: 来源: 题型:044
已知:将一副三角板(Rt△ABC和Rt△DEF)如图①摆放,点E、A、D、B在一条直线上,且D是AB的中点。将Rt△DEF绕点D顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE、AC相交于点M,直线DF、BC相交于点N,分别过点M、N作直线AB的垂线,垂足为G、H。
(1
)当α=30°时(如图②),求证:AG=DH;(2
)当α=60°时(如图③),(1)中的结论是否成立?请写出你的结论,并说明理由;(3
)当0°<α<90°时,(1)中的结论是否成立?请写出你的结论,并根据图④说明理由。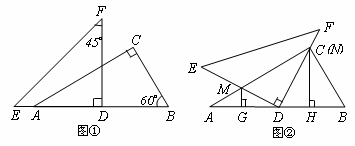
查看答案和解析>>
科目: 来源: 题型:044
如图1,△ABC为等边三角形,面积为S.D1、E1、F1分别是△ABC三边上的点,且![]() ,连结
,连结![]() 、
、![]() 、
、![]() ,可得△
,可得△![]() 是等边三角形,此时△
是等边三角形,此时△![]() 的面积
的面积![]() ,△
,△![]() 的面积
的面积![]() .
.
⑴ 当D2、E2、F2分别是等边△ABC三边上的点,且![]() 时如图2,
时如图2,
① 求证:△![]() 是等边三角形;
是等边三角形;
② 若用S表示△![]() 的面积
的面积![]() ,则S2
= ;
,则S2
= ;
若用S表示△![]() 的面积
的面积![]() ,则
,则![]() = .
= .
⑵ 按照上述思路探索下去,并填空:
当Dn、En、Fn分别是等边△ABC三边上的的点,![]() 时,(n为正整数)
时,(n为正整数)
△DnEnFn
是 三角形;若用S表示△ADnFn的面积Sn,则Sn = ;
若用S表示△DnEnFn的面积![]() ,则
,则![]() = .
= .
![]()

查看答案和解析>>
科目: 来源: 题型:044
将正六边形纸片按下列要求分割(每次分割,纸片均不得有剩余);
第一次分割:将正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
第二次分割:将第一次分割后所得的正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
按上述分割方法进行下去……
(1
)请你在下图中画出第一次分割的示意图;(2)若原正六边形的面积为![]() ,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表:
,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表:
|
分割次数(n) |
1 |
2 |
3 |
…… |
|
正六边形的面积S |
(3)观察所填表格,并结合操作,请你猜想:分割后所得的正六边形的面积S与分割次数![]() 有何关系?(S用含
有何关系?(S用含![]() 和n的代数式表示,不需要写出推理过程)。
和n的代数式表示,不需要写出推理过程)。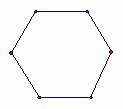
查看答案和解析>>
科目: 来源: 题型:044
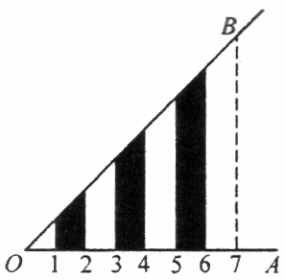
如图,![]() ,过
,过![]() 上到点
上到点![]() 的距离分别为
的距离分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的点作
的点作![]() 的垂线与
的垂线与![]() 相交,再按一定规律标出一组如图所示的黑色梯形.设前
相交,再按一定规律标出一组如图所示的黑色梯形.设前![]() 个黑色梯形的面积和为
个黑色梯形的面积和为![]() .
.
(1
)请完成下面的表格: 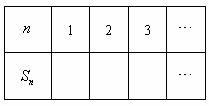
(2
)已知查看答案和解析>>
科目: 来源: 题型:044
观察下面的点阵图形和与之相对应的等式,探究其中的规律:
(1
)请你在④和⑤后面的横线上分别写出相对应的等式: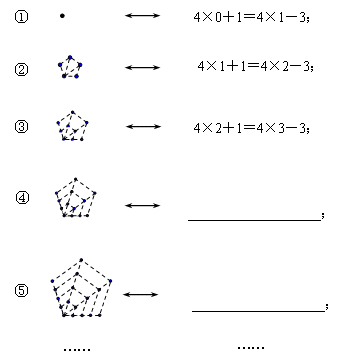
(2
)通过猜想,写出与第n个图形相对应的等式.查看答案和解析>>
科目: 来源: 题型:044
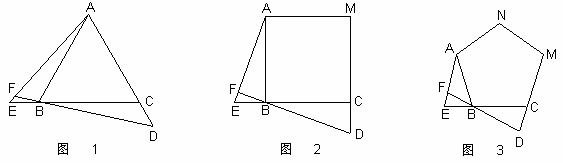
如图1、图2、图3中,点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点,一边延长线和另一边反向延长线上的点,且BE = CD,DB延长线交AE于F.
⑴求图1中,∠AFB的度数;
⑵图2中,∠AFB的度数为___________,图3中,∠AFB的度数为___________;
⑶根据前面探索,你能否将本题推广到一般的正n 边形情况。若能,写出推广问题和结论;若不能,请说明理由。
查看答案和解析>>
科目: 来源: 题型:044
两条平行直线上各有![]() 个点,用这
个点,用这![]() 对点按如下的规则连接线段;
对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当![]() 时的情况,此时图中三角形的个数为0;图2展示了当
时的情况,此时图中三角形的个数为0;图2展示了当![]() 时的一种情况,此时图中三角形的个数为2;
时的一种情况,此时图中三角形的个数为2;
(1
)当个;
(2
)试猜想当(3
)当
图1 图2 图3
查看答案和解析>>
科目: 来源: 题型:044
某校的一间阶梯教室,第1排的座位数为a,从第2排开始,每一排都比前一排增加b个座位.
⑴请你在下表的空格里填写一个适当的代数式:

⑵已知第4排有18个座位,第15排座位数是第5排座位数的2倍,求第21排有多少个座位?
查看答案和解析>>
科目: 来源: 题型:044
如图,等腰![]() 中,
中,![]() ,
,![]() 是底边上的高,
是底边上的高,![]() .
.
(1
)(2
)过点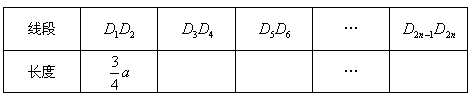
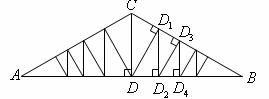
(3)某工业园区一个车间的人字形屋架为(2)中的图形,跨度![]() 为16米,
为16米,![]() 是该屋架的主柱,
是该屋架的主柱,![]() 为辅柱.若整个屋架有18根辅柱,则最短一根辅柱的长度约为多少米(结果精确到0.1米)?
为辅柱.若整个屋架有18根辅柱,则最短一根辅柱的长度约为多少米(结果精确到0.1米)?
查看答案和解析>>
科目: 来源: 题型:044
在下图中,每个正方形有边长为1 的小正方形组成:
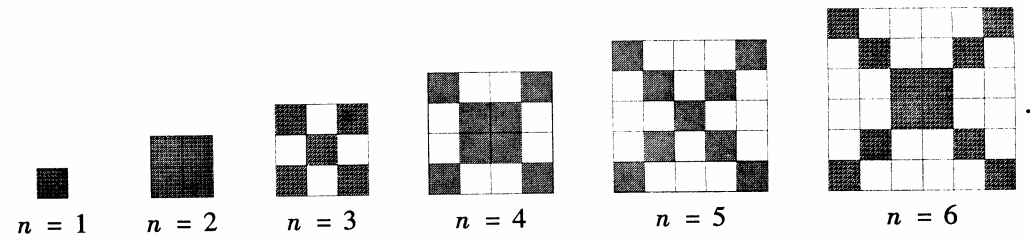
(1)观察图形,请填写下列表格:
正方形边长 | 1 | 3 | 5 | 7 | … |
|
黑色小正方形个数 | … | |||||
正方形边长 | 2 | 4 | 6 | 8 | … |
|
黑色小正方形个数 | … |
(2)在边长为![]() (
(![]() )的正方形中,设黑色小正方形的个数为
)的正方形中,设黑色小正方形的个数为![]() ,白色小正方形的个数为
,白色小正方形的个数为![]() ,问是否存在偶数
,问是否存在偶数![]() ,使
,使![]() ?若存在,请写出
?若存在,请写出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com