
科目: 来源: 题型:044
观察下面的点阵图,探究其中的规律。
摆第1个撔∥葑訑需要5个点,
摆第2个撔∥葑訑需要 个点,摆第3个撔∥葑訑需要 个点?(1)、摆第10个这样的撔∥葑訑需要多少个点?
(2
)写出摆第n个这样的撔∥葑訑需要的总点数,S与n的关系式。
查看答案和解析>>
科目: 来源: 题型:044
图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了![]() 层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为
层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]() .
.

如果图1中的圆圈共有12层,(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数![]()
![]()
![]() ,则最底层最左边这个圆圈中的数是 ;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数
,则最底层最左边这个圆圈中的数是 ;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数![]() ,
,![]() ,
,![]() ,
,![]() ,求图4中所有圆圈中各数的绝对值之和.
,求图4中所有圆圈中各数的绝对值之和.
查看答案和解析>>
科目: 来源: 题型:044
学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为![]() 的小明
的小明![]() 的影子
的影子![]() 长是
长是![]() ,而小颖
,而小颖![]() 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方![]() 点,并测得
点,并测得![]() .
.
(1
)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置(2
)求路灯灯泡的垂直高度(3
)如果小明沿线段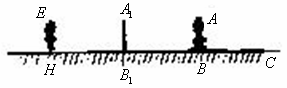
查看答案和解析>>
科目: 来源:黄冈重点作业 初三数学(下) 题型:044
如图所示,△ABC内接于⊙O,点I是△ABC的内心,连结AI并延长交BC于D,交⊙O于E,连结BE、CE.
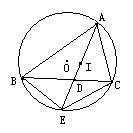
(1)若AB=2CE,AD=6,求CD的长.
(2)求证:C、I两点在以E为圆心、EB为半径的圆上.
查看答案和解析>>
科目: 来源:黄冈重点作业 初三数学(下) 题型:044
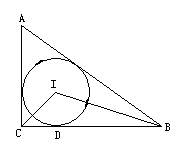
如图所示,⊙I是Rt△ABC的内切圆,且分别与BC、AC、AB相切于点D、E、F.

(1)求证:四边形IDCE是正方形;
(2)设BC=a,AC=b,AC=c,求内切圆的半径r.
查看答案和解析>>
科目: 来源: 题型:044
根据以下10个乘积,回答问题:
![]()
![]()
(1
)试将以上各乘积分别写成一个-(2
)若乘积的两个因数分别用字母(3
)若用查看答案和解析>>
科目: 来源:黄冈重点作业 初三数学(下) 题型:044
如图所示⊙I是Rt△ABC的内切圆,且∠BIC=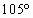 ,斜边AB=8cm,直角边BC切⊙I于点D.求:
,斜边AB=8cm,直角边BC切⊙I于点D.求:
(1)∠IBA和∠A的度数;
(2)BC和AC的长;
(3)内切圆⊙I的半径和BI的长.
查看答案和解析>>
科目: 来源: 题型:044
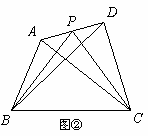
提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
(1
)当AP=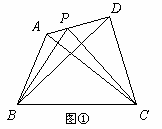
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD .
S△ABD .
∵PD=AD-AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP=![]() S△CDA .
S△CDA .
∴S△PBC =S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-![]() S△ABD-
S△ABD-![]() S△CDA
S△CDA
=S四边形ABCD-![]() (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)-![]() (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC .
S△ABC .
(2
)当AP=(3
)当AP=(4
)一般地,当AP=问题解决:当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:___________.
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:___________.
查看答案和解析>>
科目: 来源: 题型:044
如图,平面内有公共端点的六条射线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,从射线
,从射线![]() 开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
(1
)-17斣谏湎- 上.(2
)请任意写出三条射线上数字的排列规律.(3
)-2007斣谀奶跎湎呱希?/P>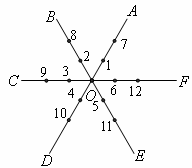
查看答案和解析>>
科目: 来源: 题型:044
如图①,![]()
![]() 为等边三角形,面积为
为等边三角形,面积为![]() .
.![]() 分别是
分别是![]() 三边上的点,且
三边上的点,且![]() ,连结
,连结![]() ,可得
,可得![]() .
.
(1
)用S表示(2
)当(3
)按照上述思路探索下去,当![]()
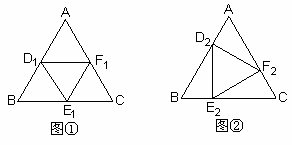
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com