
科目: 来源: 题型:044
操作与探究:
(1
)图①是一块直角三角形纸片。将该三角形纸片按如图方法折叠,是点A与点C重合,DE为折痕。试证明△CBE等腰三角形;(2
)再将图①中的△CBE沿对称轴EF折叠(如图②)。通过折叠,原三角形恰好折成两个重合的矩形,其中一个是内接矩形,另一个是拼合(指无缝无重叠)所成的矩形,我们称这样的两个矩形为“组合矩形”。你能将图③中的△ABC折叠成一个组合矩形吗?如果能折成,请在图③中画出折痕;(3
)请你在图④的方格纸中画出一个斜三角形,同时满足下列条件:①折成的组合矩形为正方形;②顶点都在格点(各小正方形的顶点)上;(4
)有一些特殊的四边形,如菱形,通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上)。请你进一步探究,一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件是,一定能折成组合矩形?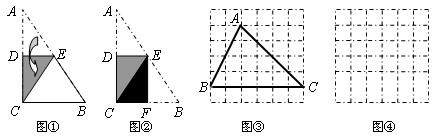
查看答案和解析>>
科目: 来源: 题型:044
问题背景;课外学习小组在一次学习研讨中,得到了如下两个命题:
①如图1,在正三角形ABC中,M,N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°.则BM=CN:
②如图2,在正方形ABCD中,M、N分别是CD、AD上的点.BM
与CN相交于点O,若∠BON=90°.则BM=CN.
然后运用类似的思想提出了如下命题:
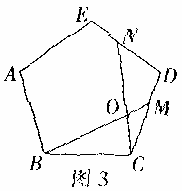
③如图3,在正五边形ABCDE中,M、N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.
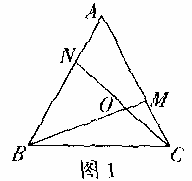



任务要求
(1)
请你从①.②,③三个命题中选择一个进行证明;(
说明:选①做对的得4分,选②做对的得3分,选③做对的得5分)(2)
请你继续完成下面的探索;①如图4,在正n(n≧3)边形ABCDEF
②如图5,在正五边形ABCDE中,M、N分别是DE,AE上的点,BM与CN相交于点O,∠BON=108°时,试问结论BM=CN是否还
成立,若成立,请给予证明.若不成立,请说明理由
(I)
我选证明:
查看答案和解析>>
科目: 来源: 题型:044
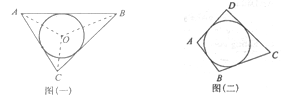
阅读材料:如图(一),△ABC的周长为![]() ,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积
,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积
∵ S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OAB=![]() ,S△OBC=
,S△OBC=![]() ,S△OCA =
,S△OCA =![]()
∴S△ABC=![]() +
+![]() +
+![]() =
=![]() (可作为三角形内切圆半径公式)
(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目: 来源: 题型:044
阅读下列材料,并解决后面的问题.
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.
过A作AD⊥BC于D(如图),

则 sinB=![]() ,sinC=
,sinC=![]() ,
,
即AD=csinB,AD=bsinC,
于是csinB=bsinC,
即![]() .
.
同理有![]() ,
,![]() .
.
所以 ![]() ………(*)
………(*)
即:在一个三角形中,各边和它所对角的正弦的比相等.
(1
)在锐角三角形中,若已知三个元素a、b、∠A,运用上述结论(*)和有关定理就可以求出其余三个未知元素c、∠B、∠C,请你按照下列步骤填空,完成求解过程:第一步:由条件 a、b、∠A ![]()
![]() ∠B;
∠B;
第二步:由条件 ∠A、∠B ![]()
![]() ∠C;
∠C;
第三步:由条件 ![]()
![]() c.
c.
(2
)如图,已知:∠A=60°,∠C=75°,a=6,运用上述结论(*)试求b.
查看答案和解析>>
科目: 来源:伴你学·数学·九年级·下册 题型:044
某校操场边有一旗杆,小芳站在操场上,距旗杆12m,当她注视旗杆顶端时,其视线的仰角为40°,此时她的双眼离地面1.5m,求该旗杆的高度(结果精确到0.01m).
查看答案和解析>>
科目: 来源: 题型:044
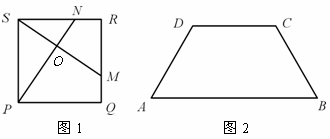
(1) 填空:如图1,在正方形PQRS中,已知点M、N分别在边QR、RS上,且QM=RN,连结PN、SM相交于点O,则∠POM=_____度 .
(2) 如图2,在等腰梯形ABCD中,已知AB∥CD,BC=CD,∠ABC=60°. 以此为部分条件,构造一个与上述命题类似的正确命题并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com