
科目: 来源: 题型:044
根据以下10个乘积,回答问题:
11×29
; 12×28; 13×27; 14×26; 15×25;16×24
; 17×23; 18×22; 19×21; 20×20.(1
)试将以上各乘积分别写成一个摗-2-○2敚?绞?椒讲睿┑男问剑?⑿闯銎渲幸桓龅乃伎脊?蹋?/P>(2
)将以上10个乘积按照从小到大的顺序排列起来;(3
)试由(1)、(2)猜测一个一般性的结论.(不要求证明)查看答案和解析>>
科目: 来源: 题型:044
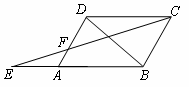
在数学课堂上,老师讲解撓嗨迫?切螖之后,接着出了一道题目让同学练习,题目是:撊缤迹?谋咝- 聪聪看后,迅速写出了下面解答: 撚- 你对聪聪的解答有何意见?为什么?![]() 是平行四边形,
是平行四边形,![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 与
与![]() 相交于
相交于![]() .请写出与
.请写出与![]() 相似的三角形,并加以证明.?/P>
相似的三角形,并加以证明.?/P>
![]() 相似的只有
相似的只有![]() .证明如下:
.证明如下:![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() .
.![]() .?/P>
.?/P>
查看答案和解析>>
科目: 来源: 题型:044
阅读下列材料,并解决后面的问题.
材料:一般地,n个相同的因数![]() 相乘:
相乘:![]() 。如23=8,此时,3叫做以2为底8的对数,记为
。如23=8,此时,3叫做以2为底8的对数,记为![]() 。
。
一般地,若![]() ,则n叫做以
,则n叫做以![]() 为底b的对数,记为
为底b的对数,记为![]() ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为![]() 。
。
问题:
(1
)计算以下各对数的值:
(2
)观察(1)中三数4、16、64之间满足怎样的关系式?(3
)由(2)的结果,你能归纳出一个一般性的结论吗?
(4
)根据幂的运算法则:证明:
查看答案和解析>>
科目: 来源: 题型:044
阅读以下材料,并解答以下问题.
“
完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法.那么完成这件事共有N= m + n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n种不同的方法, 这就是分步乘法计数原理. ”如完成沿图1所示的街道从A点出发向B点行进这件事(规定必须向北走,或向东走), 会有多种不同的走法,其中从A点出发到某些交叉点的走法数已在图2填出.(1)
根据以上原理和图2的提示, 算出从A出发到达其余交叉点的走法数,将数字填入图2的空圆中,并回答从A点出发到B点的走法共有多少种?(2)
运用适当的原理和方法算出从A点出发到达B点,并禁止通过交叉点C的走法有多少种?(3)
现由于交叉点C道路施工,禁止通行. 求如任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是多少?解: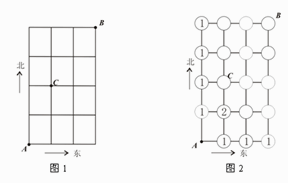
查看答案和解析>>
科目: 来源:伴你学·数学·九年级·下册 题型:044
把抛物线y=x2沿y轴向上平移3个单位能得到抛物线y=3x2吗?把抛物线y=-x2沿x轴向下平移3个单位能得到抛物线y=-3x2吗?
查看答案和解析>>
科目: 来源: 题型:044
请你先阅读下列计算过程,再回答所提出的问题:
A B C D
![]()
(2)从B到C是否正确; 。若不正确,错误的原因是
(3)请你正确解答。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com