
科目: 来源: 题型:044
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(3,0),(3,4)。动点M、N分别从O、B同时出发,以每秒1个单位的速度运动。其中,点M沿OA向终点A运动,点N沿BC向终点C运动。过点N作NP⊥AC,交AC于P,连结MP。已知动点运动了x秒。
(1
)P点的坐标为( , );(用含x的代数式表示)(2
)试求 △MPA面积的最大值,并求此时x的值。(3
)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果。

查看答案和解析>>
科目: 来源: 题型:044
如图所示,抛物线![]() 的顶点为A,直线
的顶点为A,直线![]() :
:![]() 与
与![]() 轴的交点为B,其中
轴的交点为B,其中![]() .
.
⑴ 写出抛物线对称轴及顶点A的坐标(用含![]() 的代数式表示);
的代数式表示);
⑵ 证明点A在直线![]() 上,并求出
上,并求出![]() 的度数;
的度数;
⑶ 动点Q在抛物线对称轴上,问抛物线上是否存在点P,使以P、Q、A为顶点的三角形与![]() 全等?若存在,求出
全等?若存在,求出![]() 的值,并写出所有符合上述条件的P点坐标;若不存在,说明理由.
的值,并写出所有符合上述条件的P点坐标;若不存在,说明理由.

查看答案和解析>>
科目: 来源: 题型:044
已知抛物线y=x2+(2n-1)x+n2-1 (n为常数).
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数关系式;
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C.
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时A点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:044
已知二次函数![]() 的图象经过点A(0,-2),
求证:这个二次函数图象的对称轴是x=3.题目中的矩形框部分是一段被墨水染污了无法辩认的文字.
的图象经过点A(0,-2),
求证:这个二次函数图象的对称轴是x=3.题目中的矩形框部分是一段被墨水染污了无法辩认的文字.
(1)根据已知和结论中现有的信息,你能否求出题中的二次函数解析式?若能,请写出求解过程,并画出二次函数的图象;若不能,请说明理由.
(2)请你根据已有的信息,在原题中的矩形框中,填加一个适当的条件,把原题补充完整.
查看答案和解析>>
科目: 来源: 题型:044
已知二次函数 ![]() 的图像交x轴于A、B两点,交y轴于点C.请结合这个函数的图像解决下列问题:
的图像交x轴于A、B两点,交y轴于点C.请结合这个函数的图像解决下列问题:
(1)求△ABC的面积;
(2)点P在这个二次函数的图像上运动,能使△PAB的面积等于1个平方单位的P点共有多少个?请直接写出满足条件的P点坐标;
(3)在(2)中,使△PAB的面积等于2个平方单位的P点是否存在?如果存在,写出P点的个数;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:044
已知:如图,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A( 0, 6 ),D
( 4,6),且AB=![]() .
.
(1
)求点B的坐标;(2
)求经过A、B、D三点的抛物线的解析式;(3
)在(2)中所求的抛物线上是否存在一点P,使得
查看答案和解析>>
科目: 来源: 题型:044
如图,在平面直角坐标系内,Rt△ABC的直角顶点C(0,![]() )在
)在![]() 轴的正半轴上,A、B是
轴的正半轴上,A、B是![]() 轴上是两点,且OA∶OB=3∶1,以OA、OB为直径的圆分别交AC于点E,交BC于点F.直线EF交OC于点Q.
轴上是两点,且OA∶OB=3∶1,以OA、OB为直径的圆分别交AC于点E,交BC于点F.直线EF交OC于点Q.
(1)求过A、B、C三点的抛物线的解析式;
(2)请猜想:直线EF与两圆有怎样的位置关系?并证明你的猜想.
(3)在△AOC中,设点M是AC边上的一个动点,过M作MN∥AB交OC于点N.试问:在![]() 轴上是否存在点P,使得△PMN是一个以MN为一直角边的等腰直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
轴上是否存在点P,使得△PMN是一个以MN为一直角边的等腰直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
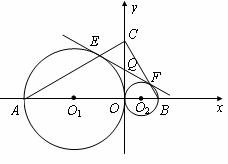
查看答案和解析>>
科目: 来源: 题型:044
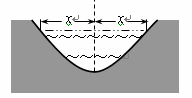
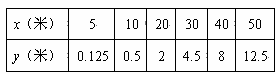
下图是某段河床横断面的示意图。查阅该河段的水文资料,得到下表中的数据:
(1
)请你以上表中的各对数据(x,y)作为点的坐标,尝试在如图所示的坐标系中画出y关于x的函数图像;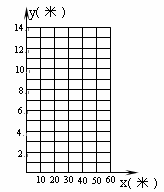
(2
)①填写下表: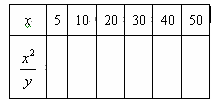
②根据所填表中数据呈现的规律,猜想出用x表示y的二次函数表达式:
(3
(3
查看答案和解析>>
科目: 来源: 题型:044
在平面直角坐标系中,A(-1,0),B(3,0).
(1) 若抛物线过A,B两点,且与y轴交于点(0,-3),求此抛物线的顶点坐标;
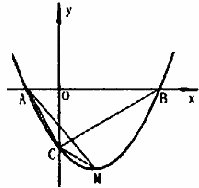
(2) 如图,小敏发现所有过A,B两点的抛物线如果与y轴负半轴交于点C,M为抛物线的顶点,那么△ACM与△ACB的面积比不变,请你求出这个比值;
(3) 若对称轴是AB的中垂线l的抛物线与x轴交于点E,F,与y轴交于点C,过C作CP∥x轴交l于点P,M为此抛物线的顶点.若四边形PEMF是有一个内角为60°的菱形,求次抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:044
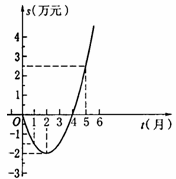
为了顺应市场要求,无为县花炮厂技术部研制开发一种新产品,年初上市后,公司经历了从亏损到盈利的过程.下面的二次函数图象(部分)刻画了该厂年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末花炮厂累积利润可达到30万元?
(3)求第8个月公司所获利润是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com