为宣传秀山丽水，在“丽水文化摄影节”前夕，丽水电视台摄制组乘船往返于丽水（A）、青田（B）两码头，在A、B间设立拍摄中心C，拍摄瓯江沿岸的景色．往返过程中，船在C、B处均不停留，离开码头A、B的距离s（千米）与航行的时间t（小时）之间的函数关系如图所示．根据图象提供的信息，解答下列问题：

(1）船只从码头A→B，航行的时间为　　 　　小时、航行的速度为　　 　　千米/时；船只从码头B→A，航行的时间为　　 　　小时、航行的速度为　　 　　千米/时；

(2）过点C作CH∥t轴，分别交AD、DF于点G、H，设AC=，GH=y，求出y与之间的函数关系式；

(3）若拍摄中心C设在离A码头25千米处， 摄制组在拍摄中心C分两组行动，一组乘橡皮艇漂流而下，另一组乘船到达码头B后，立即返回．

①求船只往返C、B两处所用的时间；

②两组在途中相遇，求相遇时船只离拍摄中心C有多远．

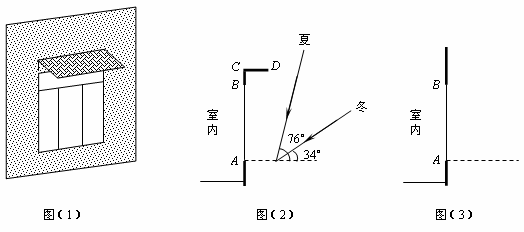
在日常生活中，我们经常看到一些窗户上安装着遮阳蓬，如图（1）.现在要为一个面向正南的窗户设计安装一个遮阳蓬，已知该地区冬天正午太阳最低时，光线与水平线的夹角为34°；夏天正午太阳最高时，光线与水平线的夹角为76°.

把图（1）画成图（2），其中AB表示窗户的高，BCD表示直角形遮阳蓬.

(1）遮阳蓬BCD怎样设计，才能正好在冬天正午太阳最低时光线最大限度地射入室内而夏天正午太阳最高时光线刚好不射入室内？请在图（3）中画图表示；

(2）已知AB=150cm，在（1）的条件下，求出BC，CD的长度（精确到1cm）.

如图所示，在平面直角坐标中，四边形OABC是等腰梯形，BC∥OA，OA=7，AB=4，∠ COA=60°，点P为x轴上的-个动点，点P不与点0、点A重合．连结CP，过点P作PD交AB于D．

(1)求点B的坐标；

(2)当点P运动什么位置时，△OCP为等腰三角形，求这时点P的坐标；

(3)当点P运动什么位置时，使得∠CPD=∠OAB，且=，求这时点P的坐标。

如下图5，AC交BD于点O，请你从下面三项中选出两个作为条件，另一个为结论，写出一个真命题，并加以证明.①OA=OC，②OB=OD，③AB∥DC.

如图，在平面直角坐标系内，已知点A（0，6）、点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒．

(1) 求直线AB的解析式；

(2) 当t为何值时，△APQ与△AOB相似？

(3) 当t为何值时，△APQ的面积为个平方单位？

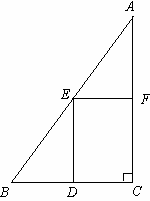
如图是某居民小区的一块直角三角形空地ABC，一直角边BC=60米，。现要利用这块空地建一个矩形停车场DCFE，使得D点在BC边上，E、F分别是AB、AC边的中点。

⑴求另一条直角边AC的长度；

⑵求停车场DCFE的面积；

⑶为了提高空地利用率，现要在剩余的△BDE中，建一个半圆形的花坛，使它的圆心在BE边上，且使花坛的面积达到最大。请你在原图中画出花坛的草图，求出它的半径（不要求说明面积最大的理由），并求此时直角三角形空地ABC的总利用率是百分之几（精确到1%）？

在△ABC中，AD为BC边上的高，∠B＝45°，∠C＝30°，AD＝2，求△ABC的面积．