
科目: 来源: 题型:044
四边形OABC是等腰梯形,OA∥BC。在建立如图的平面直角坐标系中,A (4,0),B(3,2),点M从O点以每秒3个单位的速度向终点A运动;同时点N从B点出发以每秒1个单位的速度向终点C运动,过点N作NP垂直于x轴于P点连结AC交NP于Q,连结MQ。
(1
)写出C点的坐标;(2
)若动点N运动t秒,求Q点的坐标(用含t的式子表示(3
)其△AMQ的面积S与时间t的函数关系式,并写出自变量t的取值范围。(4
)当t取何值时,△AMQ的面积最大;(5
)当t为何值时,△AMQ为等腰三角形。
查看答案和解析>>
科目: 来源: 题型:044
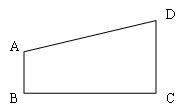
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90o,AB=4,![]() ,CD=9.
,CD=9.
(1)在BC边上找一点O,过O作OP⊥BC交AD于P,且OP2=AB-DC,求BO的长;
(2)
以BC边所在直线为x轴,OP所在直线为y轴,建立平面直角坐标系,求经过A、O、D三点的抛物线y=ax2+bx+c的解析式,并画出此抛物线的草图;(3)
在(2)中的抛物线上,连结AO、DO,证明:△AOD为直角三角形;过P点任作一直线与抛物线交于A'(x1, y1), D'(x2, y2)两点,连结
查看答案和解析>>
科目: 来源: 题型:044
如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N.
(1)设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;
(2)当AE为何值时,四边形ADNM的面积最大?最大值是多少?

查看答案和解析>>
科目: 来源: 题型:044
如图,在平行四边形ABCD中,AD=4 cm,∠A=60°,BD⊥AD. 一动点P从A出发,以每秒1 cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD .
(1) 当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2)
当点P运动2秒时,另一动点Q也从A出发沿A→B→C的路线运动,且在AB上以每秒1 cm的速度匀速运动,在BC上以每秒2 cm的速度匀速运动. 过Q作直线QN,使QN∥PM. 设点Q运动的时间为t秒(0≤t≤10),直线PM与QN截平行四边形ABCD所得图形的面积为S cm2 .① 求S关于t的函数关系式;
② (附加题) 求S的最大值.
注:附加题满分
4分,但全卷的得分不超过150分.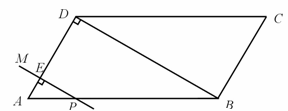
查看答案和解析>>
科目: 来源:素质教育新学案·初中几何·第三册 题型:044
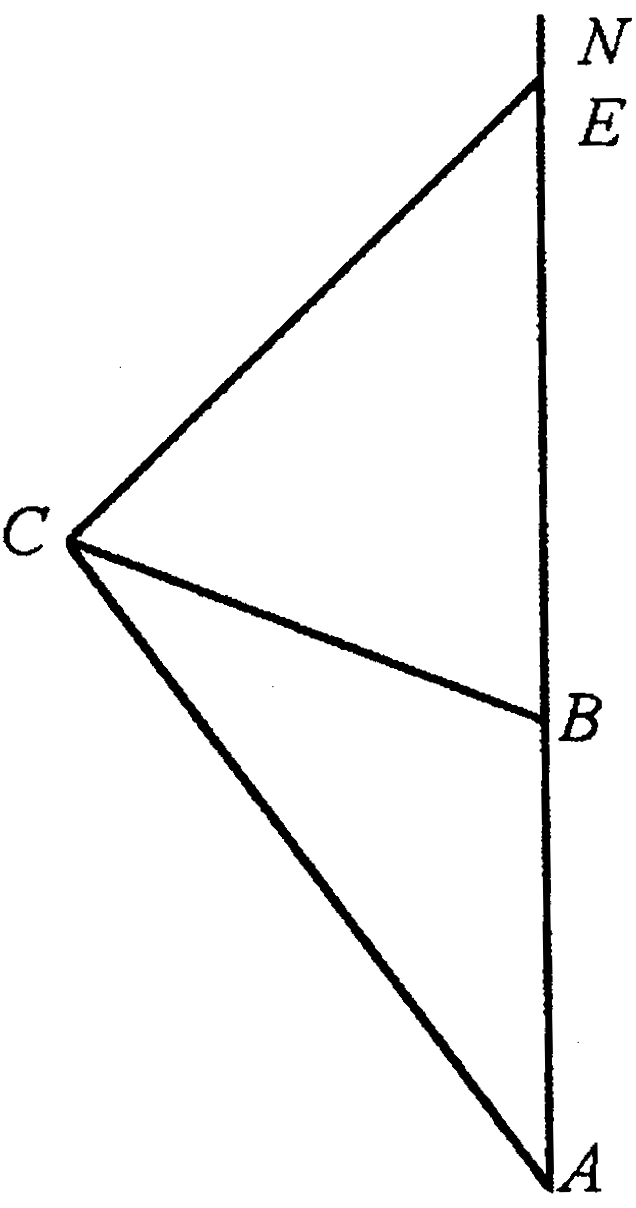
如图所示,上午8时,一条船从A处出发以15海里/时的速度向正北航行,10时到达B处,从A、B两处望灯塔C,测得∠NAC=42°,∠NBC=84°,船在B处继续前进2小时到达E,求此时船与灯塔C的距离(精确到0.01海里).
查看答案和解析>>
科目: 来源: 题型:044
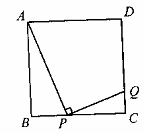
如图,正方形ABCD的边长为4cm,点P是BC边上不与点B、C重合的任意一点,连结AP,过点P作PQ⊥AP交DC于点Q,设BP的长为xcm,CQ的长为ycm。
(1)求点P在BC上运动的过程中y的最大值;
(2)当![]() cm时,求x的值。
cm时,求x的值。
查看答案和解析>>
科目: 来源: 题型:044
如图,矩形ABCD中,AB=8,BC=6,对角线AC上有一个动点P(不包括点A和点C).设AP=x,四边形PBCD的面积为y.
(1
)写出y与x的函数关系,并确定自变量x的范围.(2
)有人提出一个判断:“关于动点P,⊿PBC面积与⊿PAD面积之和为常数”.请你说明此判断是否正确,并说明理由.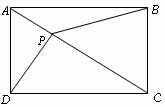
查看答案和解析>>
科目: 来源: 题型:044
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21。动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动。设运动的时间为t(秒)。
(1
)设△BPQ的面积为S,求S与t之间的函数关系式;(2
)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?(3
)当线段PQ与线段AB相交于点O,且2AO=OB时,求∠BQP的正切值;(4
)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由。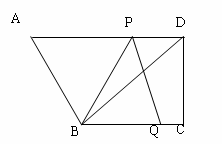
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com