
科目: 来源: 题型:044
)如图1,以矩形![]() 的两边
的两边![]() 和
和![]() 所在的直线为
所在的直线为![]() 轴、
轴、![]() 轴建立平面直角坐标系,
轴建立平面直角坐标系,![]() 点的坐标为
点的坐标为![]() 点的坐标为
点的坐标为![]() .将矩形
.将矩形![]() 绕
绕![]() 点逆时针旋转,使
点逆时针旋转,使![]() 点落在
点落在![]() 轴的正半轴上,旋转后的矩形为
轴的正半轴上,旋转后的矩形为![]() 相交于点
相交于点![]() .
.
(1
)求点(2
)将图1中的矩形(3
)如图3,当点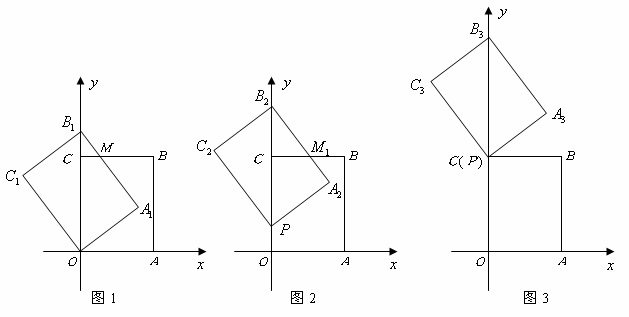
查看答案和解析>>
科目: 来源: 题型:044
如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
(1)求A、B两点的坐标;
(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;
(3)在题(2)的条件下,t为何值时,S的面积最大?最大面积是多少?

查看答案和解析>>
科目: 来源: 题型:044
如图,点O是坐标原点,点A(n,0)是x轴上一动点(n<0)。以AO为一边作矩形AOBC,使OB=2OA,点C在第二象限。将矩形AOBC绕点A逆时针旋转90°得矩形AGDE。过点A得直线y=kx+m(k≠0)交y轴于点F,FB=FA。抛物线y=ax2+bx+c过点E、F、G且和直线AF交于点H,过点H作x轴的垂线,垂足为点M。
(1)求k的值;
(2)点A位置改变使,△AMH的面积和矩形AOBC的面积比是否改变?说明你的理由。
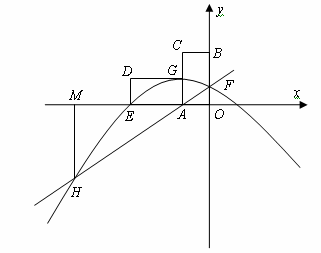
查看答案和解析>>
科目: 来源: 题型:044
如图,在矩形ABCD中,AB=3cm,BC=4cm。设P、Q分别为BD、BC上的动点,在点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P、Q移动的时间为t(0<t≤4)。
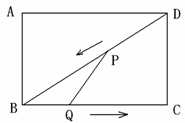
(1
)写出△PBQ的面积S(cm2)与时间t(s)之间的函数表达式,当t为何值时,S有最大值?最大值是多少?(2
)当t为何值时,△PBQ为等腰三角形?(3
)△PBQ能否成为等边三角形?若能,求t的值;若不能,说明理由。
查看答案和解析>>
科目: 来源: 题型:044
如图:正方形ABCO的边长为3,过A点作直线AD交x轴于D点,且D点的坐标为(4,0),线段AD上有一动点,以每秒一个单位长度的速度移动。
(1)求直线AD的解析式;
(2
)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P,求经过B、O、P三点的抛物线的解析式;(3
)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P1,过P1作P1E⊥x轴,垂足为E,设四边形BCEP1的面积为S,请问S是否有最大值?若有,请求出来;若没有,请说明理由。
查看答案和解析>>
科目: 来源: 题型:044
在Rt△![]() 中,
中,![]() °,
°,![]() °,
°,![]() ,等边三角形
,等边三角形![]() 从初始位置(点
从初始位置(点![]() 与点
与点![]() 重合,
重合,![]() 落在
落在![]() 上,如图1所示)在线段
上,如图1所示)在线段![]() 上沿
上沿![]() 方向以每秒1个单位的速度平移,
方向以每秒1个单位的速度平移,![]() 分别与
分别与![]() 相交于点
相交于点![]() .当点
.当点![]() 运动到点
运动到点![]() 时,△
时,△![]() 终止运动,此时点
终止运动,此时点![]() 恰好落在
恰好落在![]() 上,设△
上,设△![]() 平移的时间为
平移的时间为![]() .
.
(1)求△![]() 的边长;
的边长;
(2)求![]() 点、
点、![]() 点在
点在![]() 上的移动速度;
上的移动速度;
(3)在△![]() 开始运动的同时,如果点
开始运动的同时,如果点![]() 以每秒2个单位的速度从
以每秒2个单位的速度从![]() 点出发沿
点出发沿
![]()

查看答案和解析>>
科目: 来源: 题型:044
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0,![]() ),直线l2的函数表达式为
),直线l2的函数表达式为![]() ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
(1)
填空:直线l1的函数表达式是 ▲ ,交点P的坐标是 ▲ ,∠FPB的度数是 ▲ ;(2)
当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R=(3)
当⊙C和直线l2不相离时,已知⊙C的半径R=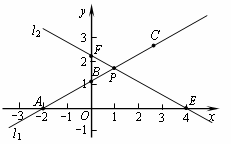
查看答案和解析>>
科目: 来源: 题型:044
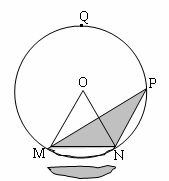
如图,在半径是2的⊙O中,点Q为优弧![]() 的中点,圆心角∠MON=60°,在
的中点,圆心角∠MON=60°,在![]() 上有一动点P,且点P到弦MN的距离为
上有一动点P,且点P到弦MN的距离为![]() 。
。
⑴求弦MN的长;(2分)
⑵试求阴影部分面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;(6分)
的取值范围;(6分)
⑶试分析比较,当自变量![]() 为何值时,阴影部分面积
为何值时,阴影部分面积![]() 与
与![]() 的大小关系(4分)
的大小关系(4分)
查看答案和解析>>
科目: 来源: 题型:044
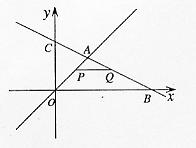
如图,在平面直角坐标系中,两个函数![]() 的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S。
的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S。
(1
)求点A的坐标。(2分)(2
)试求出点P在线段OA上运动时,S与运动时间t(秒)的关系式。(4分)(3
)在(2)的条件下,S是否有最大值?若有,求出t为何值时,S有最大值,并求出最大值;若没有,请说明理由。(2分)(4
分)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积最大时,运动时间t满足的条件是____________。(2分)查看答案和解析>>
科目: 来源:素质教育新学案·初中几何·第三册 题型:044
解答题
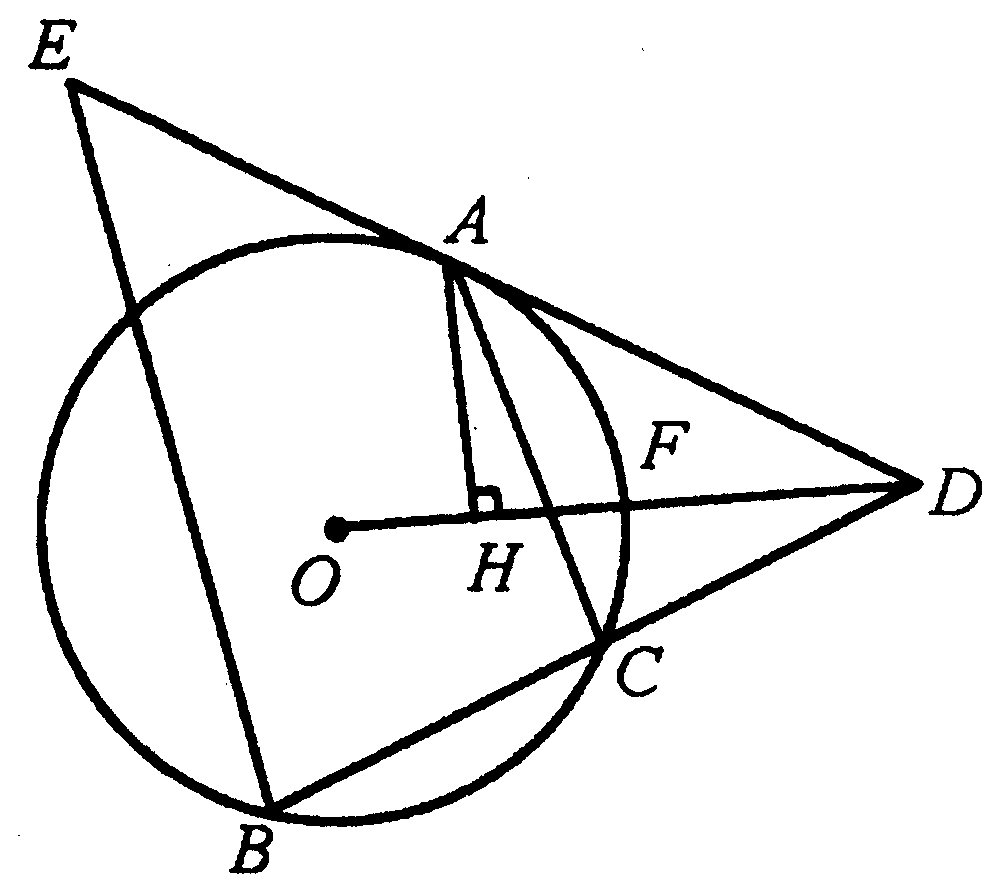
如图所示,已知割线DCB交⊙O于点C、B,DA切⊙O于点A,BE∥CA,交DA于点E,OD交⊙O于点F,AH⊥OD,垂点为H,且OH∶HF=2∶3,FD=9,![]() ,求cos∠ODB的值.
,求cos∠ODB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com