
科目: 来源: 题型:044
如图,在梯形ABCD中,AB∥CD,∠BCD=90°,且AB=1,BC=2,tan∠ADC=2.
(1) 求证:DC=BC;
(2) E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3)
在(2)的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.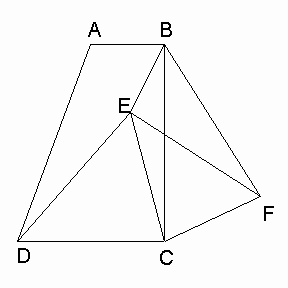
查看答案和解析>>
科目: 来源: 题型:044
如图,在平面直角坐标系中,O为坐标原点为,B(5,0),M为等腰梯形OBCD底边OB上一点,OD=BC=2,∠DMC=∠DOB=60°.
(1
)求直线CB的解析式;(2
)求点M的坐标;(3
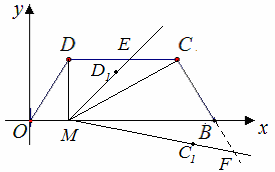
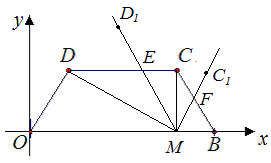
)∠DMC绕点M顺时针旋转α (30°<α<60°)后,得到∠D1MC1(点D1,C1依次与点D,C对应),射线MD1交直线DC于点E,射线MC1交直线CB于点F ,设DE=m,BF=n .求m与 n的函数关系式.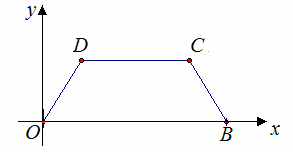
查看答案和解析>>
科目: 来源:新课标3维同步训练与评价·数学·九年级·上 题型:044
王爷爷在给小朋友分糖,分到小明,小明说:“你再给我两块糖,那么我的糖的总数的平方,等于我原有的糖的数量的9倍”你能知道小明原有几块糖吗?
查看答案和解析>>
科目: 来源: 题型:044
如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动.当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
(1)求P点从A点运动到D点所需的时间;
(2)设P点运动时间为t(秒)。
①当t=5时,求出点P的坐标;
②若⊿OAP的面积为s,试求出s与t之间的函数关系式(并写出相应的自变量t的取值范围).
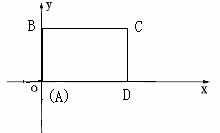
查看答案和解析>>
科目: 来源: 题型:044
在平面直角坐标系中,已知A(0,2),B(4,0),设P、Q分别是线段AB、OB上的动点,它们同时出发,点P以每秒3个单位的速度从点A向点B运动,点Q以每秒1个单位的速度从点B向点O运动.设运动时间为t(秒).

(1)
用含t的代数式表示点P的坐标;(2)
当t为何值时,△OPQ为直角三角形(3)
在什么条件下,以Rt△OPQ的三个顶点能确定一条对称轴平行于y轴的抛物线?选择一种情况,求出所确定的抛物线的解析式.查看答案和解析>>
科目: 来源: 题型:044
如图,在![]() 中,
中,![]() 所对的圆心角为
所对的圆心角为![]() ,已知圆的半径为2cm,并建立如图所示的直角坐标系.
,已知圆的半径为2cm,并建立如图所示的直角坐标系.
(1
)求圆心(2
)求经过(3
)点(4
)在(2)中的抛物线上是否存在一点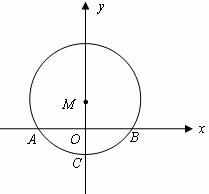
查看答案和解析>>
科目: 来源: 题型:044
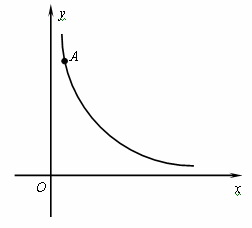
如图,在直角坐标系中,O为原点,A(4,12)为双曲线![]() (x>0)上的一点.
(x>0)上的一点.
⑴求k的值;
⑵过双曲线上的点P作PB⊥x轴于B,连接OP,若Rt△OPB两直角边的比值为![]() ,试求点P的坐标.
,试求点P的坐标.
⑶分别过双曲线上的两点P1、P2,作P1B1⊥x轴于B1,P2B2⊥x轴于B2,连结OP1、OP2.设Rt△OP1B1、Rt△OP2B2的周长分别为l1、l2,内切圆的半径分别为r1、r2,若![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:044
在平面直角坐标系中,已知矩形ABCD中,边![]() ,边
,边![]() ,且AB、AD分别在x轴、y轴的正半轴上,点A与坐标原点重合.将矩形折叠,使点A落在边DC上,设点
,且AB、AD分别在x轴、y轴的正半轴上,点A与坐标原点重合.将矩形折叠,使点A落在边DC上,设点![]() 是点A落在边DC上的对应点.
是点A落在边DC上的对应点.
⑴ 当矩形ABCD沿直线![]() 折叠时(如图1),求点
折叠时(如图1),求点![]() 的坐标和b的值;
的坐标和b的值;
⑵ 当矩形ABCD沿直线![]() 折叠时,
折叠时,
① 求点![]() 的坐标(用k表示);求出k和b之间的关系式;
的坐标(用k表示);求出k和b之间的关系式;
② 如果我们把折痕所在的直线与矩形的位置分为如图2、图3、图4所示的三种情形,请你分别写出每种情形时k的取值范围.(将答案直接填在每种情形下的横线上)k的取值范围是 ; k的取值范围是 ;k的取值范围是 ;




查看答案和解析>>
科目: 来源: 题型:044
如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点B,与直线
与x轴交于点A,与y轴交于点B,与直线![]() 交于点C.
交于点C.
⑴ 求点C的坐标;
⑵ 求△OAC的面积;
⑶ 若P为线段OA(不含O、A两点)上的一个动点,过点P作PD∥AB交直线OC于点D,连结PC.设OP
= t,△PDC的面积为S,求S与t之间的函数关系式;S是否存在最大值?如果存在,请求出来;如果不存在,请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com