
科目: 来源: 题型:044
如图,点![]() (n是正整数)依次为一次函数
(n是正整数)依次为一次函数![]() 的图像上的点,点
的图像上的点,点![]() (n是正整数)依次是x轴正半轴上的点,已知
(n是正整数)依次是x轴正半轴上的点,已知![]() ,
,![]() 分别是以
分别是以![]() 为顶点的等腰三角形。
为顶点的等腰三角形。
(1)写出![]() 两点的坐标;
两点的坐标;
(2)求![]() (用含a的代数式表示);分析图形中各等腰三角形底边长度之间的关系,写出你认为成立的两个结论;
(用含a的代数式表示);分析图形中各等腰三角形底边长度之间的关系,写出你认为成立的两个结论;
(3)当![]() 变化时,在上述所有的等腰三角形中,是否存在直角三角形?若存在,求出相应的a的值;若不存在,请说明理由。
变化时,在上述所有的等腰三角形中,是否存在直角三角形?若存在,求出相应的a的值;若不存在,请说明理由。

查看答案和解析>>
科目: 来源: 题型:044
撊?确纸菙是数学史上一个著名问题,但仅用尺规不可能撊?确纸菙 .下面是数学家帕普斯借助函数给出的一种撊?确秩窠菗的方法(如图),将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数![]() 的图象交于点P,以P为圆心,以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到得到∠MOB,则
的图象交于点P,以P为圆心,以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到得到∠MOB,则![]() .要明白帕普斯的方法,请你研究以下问题:
.要明白帕普斯的方法,请你研究以下问题:
(1)设![]() 、
、![]() ,求直线OM相对应的函数解析式(用含a,b的代数式表示).
,求直线OM相对应的函数解析式(用含a,b的代数式表示).
(2)分别过P和R作y轴和x轴的平行线,两直线相交于点Q,请说明Q点在直线OM上,据此证明![]() .
.
(3)应用上述方法得到结论,你如何三等分一个钝角(用文字简要说明).

查看答案和解析>>
科目: 来源: 题型:044
如图:已知,直线![]() ,垂足为y轴上一点A,线段OA=2,OB=1.
,垂足为y轴上一点A,线段OA=2,OB=1.
(1
)请直接写出A、B、C三点的坐标;(2
)已知二次函数(3
)(2)中的抛物线的对称轴上存在P,使△PBC为等腰三角形,请直接写出点P的坐标.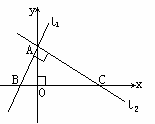
查看答案和解析>>
科目: 来源: 题型:044
如示意图,在平面直角坐标系中,O为坐标原点,点A是x轴的负半轴上一点,以AO为直径的⊙P经过点C(-8,4). 点E(m,n)在⊙P上,且-10<m≤-5,n<0,CE与x轴相交于点M,过C点作直线CN交x轴于点N,交⊙P于点F,使得△CMN是以MN为底的等腰三角形,经过E、F两点的直线与x轴相交于点Q.

(1)求出点A的坐标;
(2)当m=-5时,求图象经过E、Q两点的一次函数的解析式;
(3)当点E(m,n)在⊙P上运动时,猜想∠OQE的大小会发生怎样的变化?请对你的猜想加以证明.
解:
查看答案和解析>>
科目: 来源: 题型:044
如图,点P是x轴上一点,以P为圆心的圆分别与x轴、y轴交于A、B、C、D四点,已知A(-3,0)、B(1,0),过点C作⊙P的切线交x轴于点E.
(1)求直线CE的解析式;
(2)若点F是线段CE上一动点,点F的横坐标为m,问m在什么范围时,直线FB与⊙P相交?
(3)若直线FB与⊙P的另一个交点为N,当点N是![]() 的中点时,求点F的坐标;
的中点时,求点F的坐标;
(4)在(3)的条件下,CN交x轴于点M,求CM·CN的值.

查看答案和解析>>
科目: 来源: 题型:044
如图,直线![]() 分别与x轴、y轴交于点A、B,⊙E经过原点O及A、B两点.
分别与x轴、y轴交于点A、B,⊙E经过原点O及A、B两点.
(1)C是⊙E上一点,连结BC交OA于点D,若∠COD=∠CBO,求点A、B、C的坐标;
(2)求经过O、C、A三点的抛物线的解析式:
(3)若延长BC到P,使DP=2,连结AP,试判断直线PA与⊙E的位置关系,并说明理由.

查看答案和解析>>
科目: 来源: 题型:044
直线y= -x+m与直线y=![]() x+2相交于y轴上的点C,与x轴分别交于点A、B。
x+2相交于y轴上的点C,与x轴分别交于点A、B。
(1)求A、B、C三点的坐标;
(2)经过上述A、B、C三点作⊙E,求∠ABC的度数,点E的坐标和⊙E的半径;
(3)若点P是第一象限内的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,设∠APC=θ,试求点M、N的距离(可用含θ的三角函数式表示)。

查看答案和解析>>
科目: 来源: 题型:044
如图,在△ABC中, AB=AC=1,点D,E在直线BC上运动.点D在线段BC的左侧,点E在线段BC的右侧. 设BD = x,CE = y.
(1
)如果∠BAC = 30°,∠DAE = 105°,试确定y与x之间的函数关系式;(2
)如果∠BAC的度数为α,∠DAE的度数为β,当α,β满足怎样的关系式时,(1)中y与x之间的函数关系式还成立,试说明理由.
查看答案和解析>>
科目: 来源: 题型:044
如图,在正方形ABCD中,E是CD边的中点,AC与BE相交于点F,连接DF.
(1)
在不增加点和线的前提下,直接写出图中所有的全等三角形;(2
)连接AE,试判断AE与DF的位置关系,并证明你的结论;(3)
延长DF交BC于点M,试判断BM与MC的数量关系.(直接写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com