
科目: 来源: 题型:044
如图,AB=CD=ED,AD=EB,BE⊥DE,垂足为E.
(1)求证:△ABD≌△EDB
(2)只需添加一个条件,即________,可使四边形ABCD为矩形.请加以证明.
查看答案和解析>>
科目: 来源: 题型:044
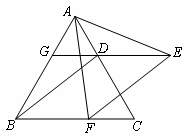
已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE、BD.
(1)求证:△AGE≌△DAB
(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.
查看答案和解析>>
科目: 来源: 题型:044
如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 为中线.现将一直角三角板的直角顶点放在点
为中线.现将一直角三角板的直角顶点放在点![]() 上并绕点
上并绕点![]() 旋转,若三角板的两直角边分别交
旋转,若三角板的两直角边分别交![]() 的延长线于点
的延长线于点![]() .
.
(1
)试写出图中除(2
)请任选一组你写出的相等线段给予证明.我选择证明 = .
查看答案和解析>>
科目: 来源: 题型:044
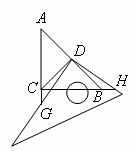
两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连结BD,取BD的中点M,连结ME,MC.试判断△EMC的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:044
(1)如图1是一个重要公式的几何解释.请你写出这个公式;
(2)如图2,![]() ,
,![]() ,且
,且![]() 三点共线.
三点共线.
试证明![]() ;
;
![]()

(3)伽菲尔德(![]() ,1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.
,1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.
查看答案和解析>>
科目: 来源: 题型:044
如图1,点A是直线y=kx(k>0,且k为常数)上一动点,以A为顶点的抛物线y=(x-h)2+m交直线y=x于另一点E,交 y 轴于点F,抛物线的对称轴交x轴于点B,交直线EF于点C.(点A,E,F两两不重合)
(1)
请写出h与m之间的关系;(用含的k式子表示)(2)
当点A运动到使EF与x轴平行时(如图2),求线段AC与OF的比值;(3)
当点A运动到使点F的位置最低时(如图3),求线段AC与OF的比值.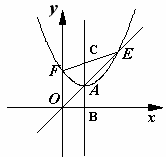
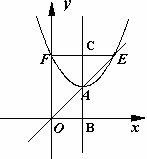

图1 图2 图3
查看答案和解析>>
科目: 来源: 题型:044
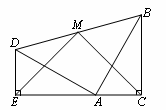
如图,在平面直角坐标系中,等腰梯形![]() 的四个顶点坐标分别为
的四个顶点坐标分别为![]() ,
,![]()
![]() .
.
(1
)求等腰梯形(2
)试说明点(3
)在第一象限内确定点
查看答案和解析>>
科目: 来源: 题型:044
如图,直线y=kx+2与x轴、y轴分别交于点A、B,点C(1,a)是直线与双曲线![]() 的一个交点,过点C作CD⊥y轴,垂足为D,且△BCD的面积为1。
的一个交点,过点C作CD⊥y轴,垂足为D,且△BCD的面积为1。
(1
)求双曲线的解析式;(2
)若在y轴上有一点E,使得以E、A、B为顶点的三角形与△BCD相似,求点E的坐标。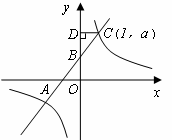
查看答案和解析>>
科目: 来源: 题型:044
已知:如图,△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P、Q两点运动即停止.点P、Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动时间为![]() (秒).
(秒).
(1)当时间![]() 为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
(2
)当点P、Q运动时,阴影部分的形状随之变化.设PQ与△ABC围成阴影部分面积为S(厘米2),求出S与时间(3
)点P、Q在运动的过程中,阴影部分面积S有最大值吗?若有,请求出最大值;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com