
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,一轮船在海上以每小时30海里的速度向正西方向航行,上午8时,在B处测得小岛A在北偏东![]() 方向上,之后轮船继续向正西方向航行,于上午9时到达C处,这时测得小岛A在北偏东
方向上,之后轮船继续向正西方向航行,于上午9时到达C处,这时测得小岛A在北偏东![]() 方向上,如果轮船继续向正西方向航行,于上午11时到达D处,这时轮船与小岛相距多远?
方向上,如果轮船继续向正西方向航行,于上午11时到达D处,这时轮船与小岛相距多远?

查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,东西方向上的A,B两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段AB),经测量,森林保护区中心P点在A城市的北偏东![]() 方向,B城市的北偏西
方向,B城市的北偏西![]() 方向上.已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内,请问,计划修筑的这条高等级公路会不会穿越保护区?为什么?
方向上.已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内,请问,计划修筑的这条高等级公路会不会穿越保护区?为什么?

查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
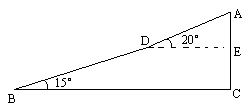
如图,一勘测人员从B点出发,沿坡角为![]() 的坡面以5千米/时的速度行至D处,用了12分钟,然后沿坡角为
的坡面以5千米/时的速度行至D处,用了12分钟,然后沿坡角为![]() 的坡面以3千米/时的速度到达山顶A点处,用了10分钟.求山高(即AC的长度)及A,B两点间的水平距离(即BC的长)(精确到0.01千米).
的坡面以3千米/时的速度到达山顶A点处,用了10分钟.求山高(即AC的长度)及A,B两点间的水平距离(即BC的长)(精确到0.01千米).
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,甲、乙两船同时从港口O出发,甲船以16.1海里/时的速度向东偏南![]() 方向航行,乙船向西偏南
方向航行,乙船向西偏南![]() 方向航行,航行了两小时,甲船到达A处并观测到B处的乙船恰好在其正西方向,求乙船的速度(精确到0.1海里/时).
方向航行,航行了两小时,甲船到达A处并观测到B处的乙船恰好在其正西方向,求乙船的速度(精确到0.1海里/时).

查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
人民海关缉私巡逻艇在东海海域执行巡逻任务时,发现在其所处位置O点的正北方向10海里的A点有一涉嫌走私船只,正以24海里/时的速度向正东方向航行,为迅速实行检查,巡逻艇调整好航向,以26海里/时的速度追赶,在涉嫌船只不改变航向和航速的前提下,问:

(1)需几小时才能追上?(点B为追上时的位置,如图).
(2)确定巡逻艇的追赶方向(精确到![]() ).
).
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
在建筑楼梯时,设计者要考虑楼梯的安全程度,如图,虚线为楼梯的斜度线,斜度线与地板的夹角为倾角θ,一般情况下,倾角θ越小,楼梯的安全程度越高.
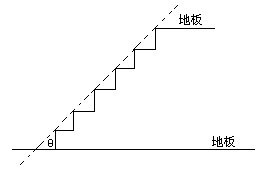
如图,设计者为提高楼梯的安全程度,要把楼梯的倾角由θ1减至θ2,这样楼梯占用地板的长度由d1增加到d2,已知d1=4米,∠θ1=![]() ,∠θ2=
,∠θ2=![]() .求楼梯占用地板的长度增加了多少?(精确到0.01米).
.求楼梯占用地板的长度增加了多少?(精确到0.01米).

查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,点A的坐标是(0.5,0),现在点A绕着点O按逆时针方向旋转,每秒钟旋转![]() ,同时点A离开O点的距离以每秒0.5个单位的速度在增大,当A点第11秒钟时到达图中的P点处,求P点的坐标.
,同时点A离开O点的距离以每秒0.5个单位的速度在增大,当A点第11秒钟时到达图中的P点处,求P点的坐标.

查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
要求![]() 的值,可构造如图所示的直角三角形进行计算.
的值,可构造如图所示的直角三角形进行计算.

作Rt△ABC,使∠C=![]() ,斜边AB=2,直角边AC=1,那么BC=
,斜边AB=2,直角边AC=1,那么BC=![]() ,∠ABC=
,∠ABC=![]() ,∴
,∴![]() =
=![]() =
=![]() =
=![]() .
.
在此图的基础上,通过添加适当的辅助线,可求出![]() 的值.请简要写出你添加的辅助线和求出的
的值.请简要写出你添加的辅助线和求出的![]() 的值.
的值.
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,某建筑物BC直立于水平地面,AC=9米,要建造阶梯AB,使每阶高不超过20厘米,最后一阶的高不足20厘米时,可按一阶计算.

(1)此阶梯至少要建多少阶?
(2)若在阶梯上铺上地毯,地毯至少要多少米?(精确到米).
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
(1)我们知道山坡的坡角越大,则坡越陡,联想到课本中的结论:tanA的值越大,则坡越陡,我们会得到一个锐角逐渐变大时,它的正切值随着这个角的变化而变化的规律,请你写出这个规律:________.
(2)如图,在Rt△ABC中,∠B=![]() ,AB=a,BC=b(a>b),延长BA、BC,使AE=CD=c,直线CA、DE交于点F.请运用上题中得到的规律并根据以上提供的几何模型证明你提炼出的不等式.
,AB=a,BC=b(a>b),延长BA、BC,使AE=CD=c,直线CA、DE交于点F.请运用上题中得到的规律并根据以上提供的几何模型证明你提炼出的不等式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com