
科目: 来源:活学巧练 九年级数学 下 题型:044
有一块铁皮,拱形边缘呈抛物线状,MN=4分米,抛物线顶点处到边MN的距离是4分米,要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在边MN上,A、D落在抛物线上,像这样截下的矩形铁皮的周长能否等于8分米?(提示:以MN所在的直线为x轴建立适当的直角坐标系)

查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
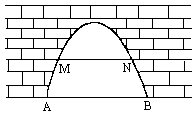
如图,是一座抛物线形拱桥,水位在AB位置时,水面宽4![]() 米,水位上升3米达到警戒线MN位置时,水面宽4
米,水位上升3米达到警戒线MN位置时,水面宽4![]() 米,某年发洪水,水位以每小时0.25米的速度上升,求水过警戒线后几小时淹到拱桥顶?
米,某年发洪水,水位以每小时0.25米的速度上升,求水过警戒线后几小时淹到拱桥顶?
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
目前国内最大跨径的钢管混凝土拱桥——永和大桥,是南宁市又一标志性建筑物,其拱形图形为抛物线的一部分,如图(1),在正常情况下,位于水面上的桥拱跨度为350米,拱高为85米.

(1)在所给的直角坐标系中(如图(2)),假设抛物线的表达式为y=ax2+b,请你根据上述数据求出a、b的值,并写出抛物线的表达式(a、b保留两个有效数字).
(2)七月份汛期将要来临,当邕江水位上涨后,位于水面上的桥拱跨度将会减小,当水位上涨4m时,位于水面上的桥拱跨度有多大?(结果保留整数)
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
已知抛物线y=ax2+c的顶点为D(0,![]() ),且过点A(1,
),且过点A(1,![]() ),如图所示.
),如图所示.

(1)试求这条抛物线的代数表达式;
(2)点F是坐标原点O关于该抛物线顶点D的对称点,坐标为(0,![]() ),我们可以用以下方法求线段FA的长度:过点A作AA1⊥x轴,过F作x轴的平行线交AA1于点A2,则FA2=1,A2A=
),我们可以用以下方法求线段FA的长度:过点A作AA1⊥x轴,过F作x轴的平行线交AA1于点A2,则FA2=1,A2A=![]() -
-![]() =
=![]() .在Rt△AFA2中,有FA=
.在Rt△AFA2中,有FA=![]() =
=![]() .
.
已知抛物线上另一点B的横坐标为2,求线段FB的长.
(3)若点P是该抛物线上在第一象限内的任意一点,试探究线段FP的长度与点P的纵坐标的大小关系,并证明你的猜想.
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
已知点A(1,a)在抛物线y=x2上.
(1)求A点的坐标;
(2)在x轴上是否存在点P,使得△OAP是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
已知函数y=(m+2)![]() 是关于x的二次函数.求:
是关于x的二次函数.求:
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
阅读材料,解答问题:
材料 小聪设计的一个电子游戏是:一电子跳蚤从P1(-3,9)开始,按点的横坐标依次增加1的规律,在抛物线y=x2上向右跳动,得到点P2、P3、P4、P5、…(如图所示).过P1、P2、P3分别作P1H1、P2H2、P3H3垂直于x轴,垂足为H1、H2、H3.则
![]() =
=![]() -
-![]() -
-![]()
=![]() (9+1)×2-
(9+1)×2-![]() (9+4)×1-
(9+4)×1-![]() (4+1)×1=1.
(4+1)×1=1.
即△P1P2P3的面积为1.

问题:(1)求四边形P1P2P3P4和四边形P2P3P4P5的面积.
(2)猜想四边形见Pn-1PnPn+1Pn+2的面积,并说明理由.
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
二次函数y=ax2的图像如图所示.

(1)求该函数的表达式.
(2)根据图像说明:x为何值时,y随x的增大而减小;x为何值时,y随x的增大而增大;x为何值时,函数y有最大值(或最小值).
(3)如果另有一函数y=![]() x2,它的图像与该函数的图像关于x轴对称、求另一函数的表达式.
x2,它的图像与该函数的图像关于x轴对称、求另一函数的表达式.
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,在平面直角坐标系中,四边形ABCO是正方形,C点的坐标是(4,0).

(1)写出A、B两点的坐标;
(2)若E是线段BC上一点,且∠AEB=![]() ,沿AE折叠正方形ABCO,折叠后B点落在平面内F点处.请画出F点并求出它的坐标;
,沿AE折叠正方形ABCO,折叠后B点落在平面内F点处.请画出F点并求出它的坐标;
(3)若E是直线BC上任意一点,问是否存在这样的E点使正方形ABCO沿AE折叠后,B点恰好落在x轴上的某一点P处?若存在,请写出此时P点和E点的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,从一块矩形薄板ABCD上裁下一个工件GEHCPD(阴影部分),图中EF∥BC,GH∥AB,∠AEG=![]() ,∠PCF=
,∠PCF=![]() ,AG=2cm,FC=6cm,求工件GEHCPD的面积.
,AG=2cm,FC=6cm,求工件GEHCPD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com