
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,△ABC中,∠B=![]() ,AB=6cm,BC=12cm.点P从点A开始,沿AB边向点B以每秒1cm的速度移动;点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动.如果P,Q同时出发.问经过几秒钟△PBQ的面积最大?最大面积是多少?
,AB=6cm,BC=12cm.点P从点A开始,沿AB边向点B以每秒1cm的速度移动;点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动.如果P,Q同时出发.问经过几秒钟△PBQ的面积最大?最大面积是多少?

查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,在Rt△ABC中,∠ACB=![]() ,AB=10,BC=8,点D在BC上运动(不运动至B,C),DE∥AC,交AB于E.设BD=x,△ADE的面积为y.
,AB=10,BC=8,点D在BC上运动(不运动至B,C),DE∥AC,交AB于E.设BD=x,△ADE的面积为y.
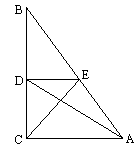
(1)求y与x的函数关系式及自变量x的取值范围;
(2)x为何值时,△ADE的面积最大?最大面积是多少?
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,已知△ABC是一等腰三角形铁板余料,其中AB=AC=20cm,BC=24cm.若在△ABC上截出一矩形零件DEFG,使EF在BC上,点D、G分别在边AB、AC上.
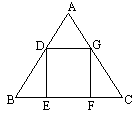
问矩形DEFG的最大面积是多少?
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.
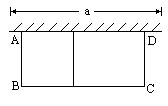
(1)如果要围成面积为45m2的花圃,AB的长是多少米?
(2)能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
如图,某市一处十字路口立交桥的截面是由抛物线和两个对称的三角形组成.其中抛物线![]() 可以用y=-
可以用y=-![]() x2+8表示,线段CD和
x2+8表示,线段CD和![]() 为两段对称的上桥斜坡,其坡度为1∶4.AD和
为两段对称的上桥斜坡,其坡度为1∶4.AD和![]() 是两侧的支柱,OA和
是两侧的支柱,OA和![]() 为两个方向的汽车通行区,宽都为15米.
为两个方向的汽车通行区,宽都为15米.

(1)求![]() 的长;
的长;
(2)BE和![]() 为支撑斜坡的立柱,其高都为4米,相应的AB和
为支撑斜坡的立柱,其高都为4米,相应的AB和![]() 为两个方向的行人及非机动车通行区,试求AB和
为两个方向的行人及非机动车通行区,试求AB和![]() 的宽;
的宽;
(3)按规定,汽车通过该桥下时,载货最高处和桥拱之间的距离不得小于0.4米,今有一大型运货汽车,装载某大型设备后,其宽为4米,车载大型设备的顶部与地面的距离均为7米,那么这辆运货汽车能否从OA(或![]() )区域安全通过?请说明理由.
)区域安全通过?请说明理由.
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
在生产中,为了节约原材料,加工某些零件时常利用一些边角余料,如图,△ABC为锐角三角形废料.基中BC=12cm,BC边上的高AD=8cm,在△ABC上截取矩形PQMN,使QM与BC边重合,试说明P,Q两点落在什么位置时,才可使它的面积S最大?最大值是多少?此时矩形的长和宽又各是多少?
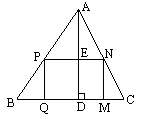
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
启明公司生产某种产品,每件成本是3元,售价是4元,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x(万元)时,产品的年销售量是原销售量的y倍,且y=-![]() +
+![]() x+
x+![]() ,如果把利润看作是销售总额减去成本和广告费:
,如果把利润看作是销售总额减去成本和广告费:
(1)试写出年利润s(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大?最大年利润是多少万元?
(2)把(1)中的最大利润留出3万元做广告,其余的资金投资新项目,现有6个项目可供选择,各项目每股投资金额和预计年收益如下表:
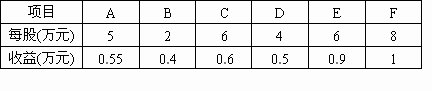
如果每个项目只能投一股,且要求所有投资项目的收益总额不得低于1.6万元,问有几种符合要求的投资方式?写出每种投资方式所选的项目.
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
某商店购进一批单价为16元的日用品,销售一段时间后,为了获取更多利润,商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件;若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
某商人将进货单价为8元的商品,按每件10元出售时,每天可销售100件,现在他想采取提高售出价的办法来增加利润,已知这种商品每提价1元/件时,日销售量就减少10件,请问他的这种想法能否实现?如果能,他把价格定为多少元时,才能使每天的获利最大?每天的最大利润是多少?如果不能,请说明理由.
查看答案和解析>>
科目: 来源:活学巧练 九年级数学 下 题型:044
某公司生产的A种产品,它的成本是2元,售价是3元,年销售量为100万件.为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费是x(十万元)时,产品的年销售量将是原销售量的y倍,且y=-![]() x2+
x2+![]() x+1.如果把利润看成是销售总额减去成本费和广告费.
x+1.如果把利润看成是销售总额减去成本费和广告费.
(1)试写出年利润s(十万元)与广告费x(十万元)的函数关系式.
(2)如果投入广告费为10万~30万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增大?
(3)在(2)中,投入的广告费为多少万元时,公司获得的年利润最大?是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com