将10分解为两数之和，设其中的一个数为x，两数之积为y．

(1)用函数表达式表示：y＝________；

(2)用表格表示：

(3)用图像表示；

(4)根据以上三种表示方式回答下列问题．

①自变量x的取值范围是什么？

②图像的对称轴和顶点坐标分别是什么？

③如何描述y随x的变化而变化的情况？

④当x取何值时，两个数的积达到最大？最大积是多少？

用长为12m的栅栏围成一个长方形花圃，花圃ABCD的一边AD靠墙(墙足够长)，设AB长为xm，长方形ABCD的面积为Sm²．

(1)用函数表达式表示：S＝________；

(2)用表格表示：

(3)用图像表示；

(4)根据以上三种表示方式回答下列问题．

①自变量x的取值范围是什么？

②图像的对称轴和顶点坐标分别是什么？

③如何描述S随x的变化而变化的情况？

④当x取何值时，长方形的面积最大？它的最大面积是多少？

图1是棱长为a的小正方体，图2，图3由这样的小正方体摆放而成，按照这样的方法继续摆放，自上而下分别叫第一层，第二层，……，第n层，第n层的小正方体的个数记为S，解答下列问题．

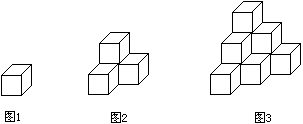
(1)按照要求填表：

(2)写出当n＝10时，S＝________；

(3)据上表中的数据，把S作为纵坐标n作为横坐标，在平面直角坐标系中描出相应的各点；

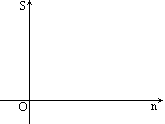
(4)请你猜一猜上述各点会在某一个函数图像上吗？如果在某一函数图像上，求出该函数的表达式．

已知二次函数y＝x²＋bx＋c的图像经过点A(C，0)，……求证这个二次函数的图像关于直线x＝2对称，其中省略号部分是一段被墨水污染了无法辨认的文字，根据现有信息，请你确定题中二次函数的可能的表达式，并说明理由．

画出函数y＝－(x＋1)²与y＝－(x－1)²的图像，

(1)完成下表：

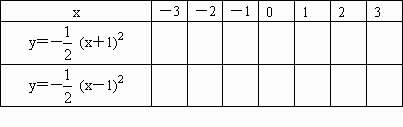
(2)在下图中作出二次函数y＝－(x＋1)²与y＝－(x－1)²的图像．

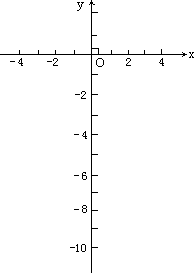
(3)函数y＝－(x＋1)²与y＝－(x－1)²的图像之间有什么关系？它是轴对称图形吗？它们的对称轴和顶点坐标分别是什么？

(4)随x的增大y分别是如何变化的？

　　在同一直角坐标系下画出下列二次函数的图像：

　　y＝x²　y＝x²＋2　y＝x²－2

　　观察三条抛物线的相互关系，并分别指出它们的开口方向及对称轴、顶点的位置，你能说出抛物线y＝x²＋k的开口方向及对称轴、顶点的位置吗？

正方形A的边长为a，正方形B的边长是2a，

(1)分别写出两个正方形的面积S与边长之间的关系式；

(2)在同一直角坐标系下，作出两个函数图像；

(3)观察两个图像，找出相同点与不同点．

二次函数y＝－3x²＋1的图像与二次函数y＝－3x²的图像有什么关系？它是轴对称图形吗？它的开口方向、对称轴和顶点坐标分别是什么？先想一想，如果需要，作草图看一看，二次函数y＝－x²＋1与y＝－x²呢？

一块四周镶有宽度相等的花边的地毯如图所示，它的长为8m，宽为5m，如果设花边的宽为x(m)，地毯中央长方形图案的面积分别为y(cm²)：

(1)写出y与x之间的函数关系式；

(2)当花边的宽分别10cm，20cm时，地毯中央长方形图案的面积为多少？

(3)当花边的宽度为多少时，地毯中央长方形图案的面积为28m²？

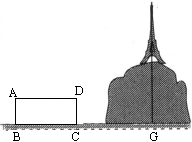
如图，山上有一座铁塔，山脚下有一矩形建筑物ABCD，且建筑物周围没有开阔平整地带，该建筑物顶端宽度AD和高度DC都可直接测得，从A，D，C三点可以看到顶端H．可供选择的测量工具有皮尺、测倾器．

(1)请你根据现有条件，充分利用矩形建筑物，设计一个测量塔顶端到地面高度HG的方案．具体要求如下：

①测量数据尽可能少；

②在所给图形上，画出你设计的测量平面图，并将应测数据标记在图形上(如果测线段用m，n表示；如果测角用α，β，γ表示，测倾器高度不计)．

(2)根据你测量的数据，计算塔顶端到地面的高度HG(用字母表示)．   

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　   H