如图，一位农夫现要将一块矩形土地用篱笆分成三个全等的小矩形，篱笆总长为120m．

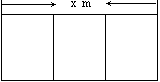
(1)矩形土地的总面积S与其长x之间的关系式；

(2)当x为多少m时，矩形面积S最大？最大是多少？

如图，有长为40m的篱笆，一面利用墙(墙的最大可用长度a为15m)，围成长方形花圃，设花圃的长BC为xm，面积为Sm²．

(1)求S与x的函数关系式；

(2)如果要围成面积为182m²的花圃，BC的长是多少米？

(3)能围成面积比182m²更大的花圃吗？如果能，请求出最大面积，并说明围法，如果不能，请说明理由．

某软件商店经销一种销售成本为40元的益智游戏软件，根据市场分析，若按每盘50元销售，一个月能售出500盘，销售单价每涨1元，月销售量就减少10盘，设销售单价为每盘x元时，月销售利润为y元．

(1)求y与x之间的函数关系式；

(2)当销售单价定为多少元时，月销售利润最高？

(3)当销售单价定为每盘55元时，计算月销量和月销售利润；

(4)商店想在销售成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应定为多少？

(5)若使销售利润超过8000元，涨价幅度应在什么范围内？

某商场销售一批名优童装，平均每天可销售20套，每套盈利40元，为了扩大销售，增加盈利尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果一套童装每降价1元，商场平均每天可多售出2套．

(1)设每套童装降价x元，求x的取值范围；

(2)每套童装降价多少元时，商场平均每天盈利最多？

(3)若商场平均每天要盈利1200元，每套童装应降价多少元？

(4)要使利润高于1200元，降价幅度应在什么范围内？

某商场以每件30元的价格购进一种商品，试销中发现，这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数：m＝162－3x．

(1)写出商场卖这种商品每天的销售利润y与每件的销售价x间的函数关系式；

(2)如果商场要想每天获得最大的销售利润，每件商品的售价定为多少最合适？最大销售利润为多少？

某玩具厂计划生产一种玩具熊猫，每日最高产量为40只，且每日产出的产品全部售出，已知生产x只玩具熊猫的成本为R(元)，售价每只为P(元)，且R，P与x的关系式分别是R＝500＋30x，P＝170－2x．

(1)当日产量为多少时，每日获得的利润为1750元？

(2)当日产量为多少时，可获得最大利润？最大利润是多少？

某商场销售一批名牌衬衫平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．

(1)若商场平均每天要盈利1200元，每件衬衫降价多少元？

(2)若为尽快减少库存，每件衬衫降价多少元时，商场平均每天盈利最多？

某果园有100棵桃树，一棵桃树平均结1000个桃子，现准备多种一些桃树以提高产量，试验发现，每多种一棵桃树，每棵桃树的产量就会减少2个，设多种x棵桃树，那么：

(1)现在果园桃树的棵数可以表示为________；

(2)现在每棵桃树的产量可以表示为________；

(3)现在果园桃树的总产量可以表示为________；

(4)当多种________棵桃树时，桃子的总产量最大，最大是________．

如图，已知：△ABC中，AC＝BC＝，∠C＝，AB上有一动点P，过P作PE⊥AC，垂足为E，作PF⊥BC，垂足为F．

设CF＝x，用含x的代数式把Rt△AEP，矩形PECF及Rt△PFB的面积表示出来．

如图在矩形ABCD中，AB＝6cm，BC＝12cm，点P从A出发，沿AB边向点B以1cm/s的速度移动，同时点Q从点B出发沿BC边向点C以2cm/s的速度移动(P，Q两点在分别到达B，C两点后就停止移动)．若设运动开始后第t秒钟时，五边形APQCD的面积为Scm²．

(1)写出S与t的函数关系式；

(2)作出函数图像；

(3)根据图像回答下列问题．

①自变量t的取值范围是什么？

②图像的对称轴和顶点坐标分别是什么？

③当t为多少时，五边形的面积最小？最小是多少？