
科目: 来源: 题型:044
(2006安徽,23)(13分)取一副三角板按图①拼接,固定三角板ADC,将三板ABC绕点A依顺时针方向旋转一个大小为α的角(0°<α≤45°)得到△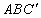 ,如图所示.
,如图所示.

试问:(1)当α为多少度时,能使得图②中AB∥DC?
(2)当旋转到图③位置,此时α又为多少度?图③中你能找出哪几对相似三角形,并求其中一对的相似比;
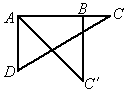
图③
(3)连结BD,当0°<α≤45°时,探寻∠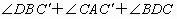 值的大小变化情况,并给出你的证明.
值的大小变化情况,并给出你的证明.
查看答案和解析>>
科目: 来源: 题型:044
(2004 四川成都)某供电部门准备在输电主干线l上连接一个分支线路,分支点为M,同时向新落成的A、B两个居民小区送电.已知居民小区A、B分别到主干线l的距离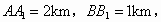 且
且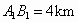 .
.
(1)如果居民小区A、B在主干线l的两旁,如图所示,那么分支点M在什么地方时总线路最短?最短线路的长度是多少千米?
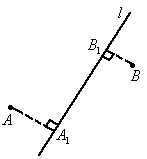
a)
(2)如果居民小区A、B在主干线l的同旁,如图所示,那么分支点M在什么地方时总线路最短?此时分支点M与的距离是多少千米?

b)
查看答案和解析>>
科目: 来源: 题型:044
(2005 江苏苏州)如图所示,等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.

(1)求证:AE∥BC;
(2)如图所示,将(1)中等边△ABC的形状改成以BC为底边的等腰三角形,所作△EDC改成相似于△ABC.请问:是否仍有AE∥BC?证明你的结论.
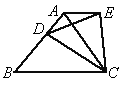
查看答案和解析>>
科目: 来源: 题型:044
(2003 江苏泰州)如图所示,将矩形ABCD(AB<AD)沿BD折叠后,点C落在点E处,且BE交AD于点F.
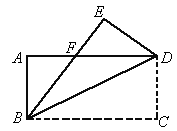
(1)若AB=4,BC=8,求DF的长;
(2)当DA平分∠EDB时,求 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:044
(2005陕西)已知:直线a∥b,P、Q是直线a上的两点,M、N是直线b上的两点.
(1)如图1,线段PM、QN夹在平行直线a和b之间,四边形PMNQ为等腰梯形,其两腰PM=QN.
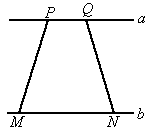
图1
请你参照图1,作图2中画出异于图1的一种图形,使夹在平行直线a和b之间的两条线段相等.

图2
(2)我们继续探究,发现用两条平行直线a、b去截一些我们学过的图形,会有两条“曲线段相等”(曲线上两点和它们之间的部分叫做“曲线段”,把经过全等变换后能重合的两条曲线段叫做“曲线段相等”).
请你在图3中画出一种图形,使夹在平行直线a和b之间的两条曲线段相等.

图3
(3)如图4,若梯形PMNQ是一块绿化地,梯形的上底PQ=m,下底MN=n,且m<n,现计划把价格不同的两种花草种植在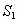 、
、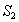 、
、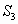 、
、 四块地里,使得价格相同的花草不相邻,为了节省费用,园艺师应选择哪两块地种植价格较便宜的花草?请说明理由.
四块地里,使得价格相同的花草不相邻,为了节省费用,园艺师应选择哪两块地种植价格较便宜的花草?请说明理由.
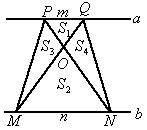
图4
查看答案和解析>>
科目: 来源: 题型:044
(2007,宁夏回族自治区,24)某家庭装修房屋,由甲、乙两个装修公司合作完成,先由甲装修公司单独装修3天,剩下的工作由甲、乙两个装修公司合作完成.工程进度满足如图所示的函数关系,该家庭共支付工资8000元.
(1)完成此房屋装修共需多少天?
(2)若按完成工作量的多少支付工资,甲装修公司应得多少元?

查看答案和解析>>
科目: 来源: 题型:044
(2007,贵阳,22)甲、乙两人骑自行车前往A地,他们距A地的路程s(km)与行驶时间t(h)之间的关系如图所示,请根据图像所提供的信息解答下列问题:
(1)甲、乙两人的速度各是多少?
(2)写出甲、乙两人距A地的路程s与行驶时间t之间的函数关系式(任写一个).
(3)在什么时间段内乙比甲离A地更近?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com