(2005·北京)如图所示，一根长2a的木棍(AB)，斜靠在与地面(OM)垂直的墙(ON)上，设木棍的中点为P，若木棍A端沿墙下滑，且B端沿地面向右滑行．

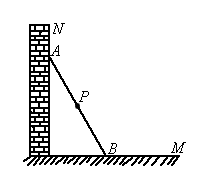
(1)请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由．

(2)在木棍滑动的过程中，当滑动到什么位置时，△AOB的面积最大？简述理由，并求出面积的最大值．

2005河南课改)如图，正方形ABCD的边长为4cm，点P是BC边上不与点B、C重合的任意一点，连结AP，过点P作PQ⊥AP交DC于点Q，设BP的长为xcm，CQ的长为ycm．

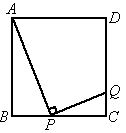
(1)求：点P在BC上运动的过程中y的最大值；

(2)当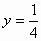cm时，求x的值．

(2004厦门)已知：正方形ABCD和正方形AEFG有一个公共点A，点G、E分别在线段AD、AB上．

(1)如图1，连结DF、BF，若将正方形AEFG绕点A按顺时针方向旋转，判断命题：“在旋转的过程中，线段DF与BF的长始终相等．”是否正确？若正确请证明；若不正确请举反例说明；

图1

(2)若将正方形AEFG绕点A按顺时针方向旋转，连结DG，在旋转的过程中，你能否找到一条线段的长与线段DG的长始终相等？并以图2为例说明理由．

图2

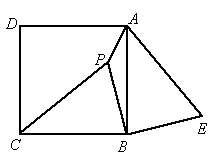
(2005·厦门)已知：如图，P是正方形ABCD内一点，在正方形ABCD外有一点E，满足∠ABE＝∠CBP，BE＝BP，

(1)求证：△CPB≌AEB；

(2)求证PB⊥BE；

(3)若PA∶PB＝1∶2，∠APB＝135°，求cos∠PAE的值．

(2005·广州)如图a，已知正方形ABCD的面积为S．

(1)求作四边形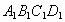，使得点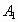和点A关于点B对称，点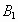和点B关于点C对称，点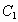和点C关于点D对称，点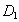和点D关于点A对称(只要求画出图形，不要求写作法)；

(2)用S表示(1)中作出的四边形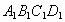的面积；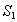

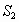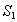(3)若将已知条件中的正方形改为任意四边形，面积仍为S，并按(1)的要求作出一个新的四边形，面积为，则与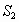是否相等?为什么?

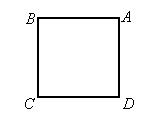
a)

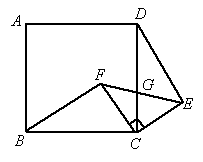
(2005·吉林)如图，四边形ABCD是正方形，△ECF是等腰直角三角形，其中CE＝CF，G是CD与EF的交点．

(1)求证：△BCF≌△DCE；

(2)若BC=5，CF=3，∠BFC＝90°，求DG∶GC的值．

(2005·山西·23)如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接BE、DG

(1)观察猜想BE与DG之间的大小关系，并证明你的结论；

(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在，请说出旋转过程；若不存在，请说明理由．

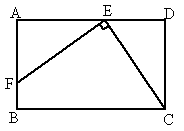
(2007，辽宁省十二市，20)如图，已知矩形ABCD中，E是AD上的一点，F是AB上的一点，EF⊥EC，且EF=EC，DE=4cm，矩形ABCD的周长为32cm，求AE的长．

(2005浙江台州)我国的代数学家秦九韶在《数书九章》中记述了“三斜求积术”，即已知三角形的三边长，求它的面积，用现代式子表示为：　①(其中a、b、c为三角形的三边长，s为面积)．而另一个文明古国古希腊也有求三角形面积的海伦公式：　②．

(1)若已知三角形的三边长分别为5、7、8，试分别运用公式①和公式②，计算该三角形的面积s；

(2)你能否由公式①推导出公式②？请试试．

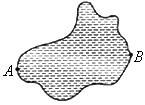
(2004甘肃灵武课改)如图，要在湖的两岸A，B间建一座观赏桥，由于条件限制，无法直接度量A，B两点间的距离．请你用学过的数学知识按以下要求设计一测量方案．

(1)画出测量图案；

(2)写出测量步骤(测量数据用字母表示)；

(3)计算AB的距离(写出来解或推理过程，结果用字母表示)