如图所示，已知⊙O与CA、CB相切于点A、B，，AB=6cm，求∠ACB的度数．

如图所示，在以O为圆心的两个同心圆中，小圆的半径长为2，大圆的弦AB与小圆交于点C、D，AC=CD，且∠COD=60°

(1)求大圆半径的长．

(2)若大圆的弦AE与小圆切于点F，求AE的长．

工人师傅为检测该厂生产的一种铁球的大小是否符合要求，设计了一个如图甲所示的工件槽，其中工件槽的两个底角均为90°，尺寸如图甲(单位：cm)．将形状规则的铁球放入槽内时，若同时具有图甲所示的A、B、E三个接触点，该球的大小就符合要求．

图乙是过球心O及A，B，E三点的截面示意图．已知⊙O的直径就是铁球的直径，AB是⊙O的弦，CD切GO于点E,AC⊥CD，BD⊥CD．请你结合图甲中的数据，计算这种铁球的直径．

如图所示，在锐角△ABC中，BA＝BC，点O是边AB上的一个动点(不与点A、B重合)，以O为圆心，OA为半径的圆交边AC于点M，过点M作⊙O的切线MN交BC于点N

(1)当OA=OB时，求证：MN⊥BC；

(2)分别判断OA＜OB、OA＞OB，上述结论是否成立?请选择一种情况说明理由．

已知：如图所示，AB是⊙O的直径，P是AB上的一点(与A、B不重合)，QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D，则△CDQ是等腰三角形．对上述命题证明如下：

证明：连接OC．

∵OA=OC，

∴∠A＝∠1．

∵CD切⊙O于C点，

∴∠OCD＝90°．

∴∠1＋∠2＝90°．

∴∠A＋∠2=90°．

在Rt△QPA中，∠QPA＝90°，

∴∠A＋∠Q=90°．

∴∠2=∠Q．∴DQ＝DC．

即△CDQ是等腰三角形

问题：对上述命题，当点P在BA的延长线上时，其他条件不变，结论“△CDQ是等腰三角形”还成立吗?若成立，请给予证明；若不成立，请说明理由．

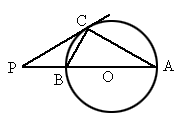
如图所示，AB是⊙O的直径，P是AB的延长线上的一点，PC切⊙O于点C，⊙O的半径为3，∠PCB＝30°．

(1)求∠CBA的度数；

(2)求PA的长．

如图所示，AB是⊙O的直径，⊙O过AC的中点D，DE⊥BC，垂足为E．

(1)由这些条件，你能推出哪些正确结论？(要求：不再标注其它字母，找结论的过程中所连辅助线不能出现在结论中，不写推理过程，写出个结论即可)．

(2)若∠ABC为直角，其他条件不变，除上述结论外，你还能推出哪些结论？

如图所示，AB是⊙O的直径，P为AB的延长线上一点，PD切⊙O于点C，BC和AD的延长线相交于点E，且AD⊥PD．

(1)求证：AB＝AE；

(2)当AB：BP为何值时，△ABE为等边三角形?并说明理由．

正方形网格中，每个小正方形的边长为1个单位，以O为原点建立平面直角坐标系，圆心A(3，0)的⊙A被y轴截得的弦长BC=8，如图所示，解答下列问题：

(1)⊙A的半径为________．

(2)请在图中将⊙A先向上平移6个单位，再向左平移8个单位得到⊙D，观察你所画的图形知⊙D点的坐标是________；⊙D与x轴的位置关系是________；⊙D与y轴的位置关系是________．

台风是一种自然灾害，它以台风中心为圆心在周围数十千米范围内形成气旋风暴，有极强的破坏力．如图，据气象观测，距沿海某城市A的正南方向220千米B处有台风中心，其中心最大风力为12级，每远离台风中心20千米，风力就会减弱一级，该台风中心现正以15千米/时的速度沿北偏东30°方向往C移动，且台风中心风力不变．若城市所受风力达到或超过四级，则称为受台风影响．问该城市是否会受到这次台风的影响？请说明理由．