“青朱出入图”真是“无字的证明”．如图所示也是一种“无字证明”方法．做法是：过较大正方形的中心，作两条互相垂直的线，将其分成4份．然后，将这四个部分围在四周，小正方形填在中间，恰好得到大正方形．当然，“两条互相垂直的线”可有很多，你如何选择一条恰当的呢？亲自做一做，你可能会有更多的收获！

意大利文艺复兴时代的著名画家达·芬奇对勾股定理也曾进行了研究．他验证勾股定理的方法可以从下面的实验中得到体现．

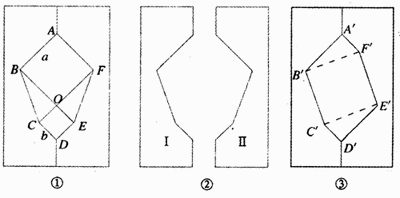
(1)在一张长方形的纸板上画两个边长分别为a，b的正方形，并连接BC，FE(如图①所示)．

(2)沿ABCDEFA剪下，得到两个大小相同的纸板Ⅰ，Ⅱ，如图②所示．

(3)将纸板Ⅱ翻转后与Ⅰ拼成如图③所示的图形．

(4)比较图①，图③中两个多边形ABCDEF和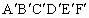的面积，你能验证勾股定理吗？请动手做一做．

如图，某隧道的截面是一个半径为3.6米的半圆形，一辆高2.4米、宽3米的卡车能通过该隧道吗？

在一张纸上复制四个全等的直角三角形，通过拼图的方法验证勾股定理．你有哪些方法？并说说你的方法与课堂上方法之间有什么联系与差别．

如图是美国总统Garfield于1876年给出的一种验证勾股定理的办法，你能利用它验证勾股定理吗？说一说这个方法和本节的探索方法的联系．

如图，求等腰△ABC的面积．

求斜边长17厘米、一条直角边长15厘米的直角三角形的面积．

求出下列直角三角形中未知边的长度．

(1)观察：4×6＝24，

　　　　14×16＝224．

　　　　24×26＝624，

　　　　34×36＝1224，

　　你发现其中的规律了吗？你能用代数式表示这一规律吗？

(2)利用(1)中的规律计算124×126．

(3)你还能找到类似的规律吗？

(1)估计100万枚1元硬币摞在一起大约有多高．

(2)“一个人一辈子活了100万时．”你认为可能吗？为什么？