
科目: 来源:中考必备’04全国中考试题集锦·数学 题型:044
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=![]() ,BC=1.连结BF,分别交AC、DC、DE于点P、Q、R.
,BC=1.连结BF,分别交AC、DC、DE于点P、Q、R.
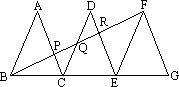
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的问题,并进行解答(根据提出问题的层次和解答过程评分).
查看答案和解析>>
科目: 来源:中考必备’04全国中考试题集锦·数学 题型:044
在平面直角坐标系中,A(-1),B(3,0).
(1)若抛物线过A,B两点,且与y轴交于点(0,-3),求此抛物线的顶点坐标;
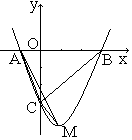
(2)如图,小敏发现所有过A,B两点的抛物线如果与y轴负半轴交于点C,M为抛物线的顶点,那么△ACM与△ACB的面积比不变,请你求出这个比值;
(3)若对称轴是AB的中垂线l的抛物线与x轴正车轴交于点E,F,与y轴交干点C,过C作CP∥x轴交l于点P,M为此抛物线的顶点.若四边形PEMF是有一内角为![]() 的菱形,求此抛物线的解析式.
的菱形,求此抛物线的解析式.
查看答案和解析>>
科目: 来源:中考必备’04全国中考试题集锦·数学 题型:044
在△ABC中,AB=AC,D为BC上一点.由D分别作DE⊥AB于E,DF⊥AC于F;设DE=a,DF=b,且实数a,b满足9a2-24ab+16b2=0,并有2![]() =2566;∠A使得方程
=2566;∠A使得方程![]() x2-x·sinA+
x2-x·sinA+![]() sinA-
sinA-![]() =0有相等的两个实数根.
=0有相等的两个实数根.
(1)试求实数a,b的值;
(2)试求线段BC的长.
查看答案和解析>>
科目: 来源:中考必备’04全国中考试题集锦·数学 题型:044
已知:如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3)BC=2AB,P为AD边上一动点(与点A、D不重合),以点P为圆心作⊙P与对角线AC相切于点F,过P、F作直线l,交BC边于点E.当点P运动到点P1位置时,直线l恰好经过点B此时直线的解析式是y=2x+1.
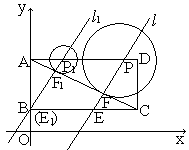
(1)求BC、AP1的长;
(2)设AP=m,梯形PECD的面积为S,求S与m之间的函数关系式,写出自变量m的取值范围;
(3)以点E为圆心作⊙E与x轴相切.
①探究并猜想:⊙P和⊙E有哪几种不同的位置关系?并求出AP相应的取值范围;
②当直线l把矩形ABCD分成两部分的面积之比为3∶5时,则⊙P和⊙E的位置关系如何?并请说明理由.
查看答案和解析>>
科目: 来源:中考必备’04全国中考试题集锦·数学 题型:044
小刚为书房买灯.现有两种灯可供选购,其中一种是9瓦(即0.009千瓦)的节能灯,售价49元/盏;另一种是40瓦(即0.04千瓦)的白炽灯,售价18元/盏.假设两种灯的照明亮度一样,使用寿命都可以达到2800小时.已知小刚家所在地的电价是每千瓦时0.5元.
(1)设照明时间是x小时,请用含x的代数式分别表示用一盏节能灯的费用和用一盏白炽灯的费用;(注:费用=灯的售价+电费)
(2)小刚想在这两种灯中选购一盏.
①当照明时间是多少时,使用两种灯的费用一样多?
②试用特殊值判断:
照明时间在什么范围内,选用白炽灯费用低?
照明时间在什么范围内,选用节能灯费用低?
(3)小刚想在这两种灯中选购两盏.
假定照明时间是3000小时,使用寿命是2800小时.请你帮他设计一种费用最低的选灯方案,并说明理由.
查看答案和解析>>
科目: 来源:中考必备’04全国中考试题集锦·数学 题型:044
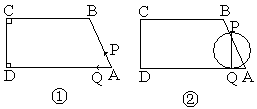
如图1,在直角梯形ABCD中,∠D=∠C=![]() ,AB=4,BC=6,AD=8.点P、Q同时从A点出发,分别作匀速运动,其中点P沿AB、BC向终点C运动,速度为每秒2个单位,点Q沿AD向终点D运动,速度为每秒1个单位.当这两点中有一个点到达自己的终点时,另一个点也停止运动,设这两点从出发运动了t秒.
,AB=4,BC=6,AD=8.点P、Q同时从A点出发,分别作匀速运动,其中点P沿AB、BC向终点C运动,速度为每秒2个单位,点Q沿AD向终点D运动,速度为每秒1个单位.当这两点中有一个点到达自己的终点时,另一个点也停止运动,设这两点从出发运动了t秒.
(1)动点P与Q哪一点先到达自己的终点?此时t为何值?
(2)当0<t<2时,求证:以PQ为直径的圆与AD相切(如图2);
(3)以PQ为直径的圆能否与CD相切?若有可能,求出t的值或t的取值范围;若不可能,请说明理由.
查看答案和解析>>
科目: 来源:中考必备’04全国中考试题集锦·数学 题型:044
已知抛物线y=(1-m)x2+4x-3开口向下,与x轴交于A(x1,0)和B(x2,0)两点,其中x1<x2.

(1)求m的取值范围;
(2)若![]() +
+![]() =10,求抛物线的解析式,并在给出的直角坐标系中画出这条抛物线;
=10,求抛物线的解析式,并在给出的直角坐标系中画出这条抛物线;
(3)设这条抛物线的顶点为C,延长CA交y轴于点D.在y轴上是否存在点P,使以P、O、B为顶点的三角形与△BCD相似?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:中考必备’04全国中考试题集锦·数学 题型:044
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(3,0)、(3,4).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于点P,连结MP.已知动点运动了x秒.
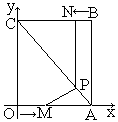
(1)P点的坐标为(________,________);(用含x的代数式表示)
(2)试求△MPA面积的最大值,并求此时x的值;
(3)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果.
查看答案和解析>>
科目: 来源:中考必备’04全国中考试题集锦·数学 题型:044
如图,抛物线y=ax2+bx+c与y轴相交于点C(0,1),x1,x2是方程ax2+bx+c=x的两个根,且x1=-x2.点A(x1,0)在点B(x2,0)的左边,以AB为直径的圆交y轴于C,D两点.
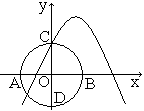
(1)求抛物线y=ax2+bx+c的解析式;
(2)设抛物线的对称轴交x轴于E点,连结CE并延长交圆于F点,求EF的长;
(3)过D点作圆的切线交直线CB于点P,判断点P是否在抛物线上说明理由.
查看答案和解析>>
科目: 来源:中考必备’04全国中考试题集锦·数学 题型:044
三角形纸片ABC,∠C=![]() ,AB=2BC=12.将纸片折叠使点A总是落在BC边上,记为点D,EF是折痕,如图.
,AB=2BC=12.将纸片折叠使点A总是落在BC边上,记为点D,EF是折痕,如图.
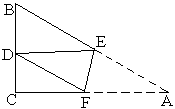
(1)当△DEF是以∠EDF为顶角的等腰三角形时,求△DCF的面积;
(2)在BC边上是否存在一点D,使以D,E,F为顶点的三角形和以D,E,B为顶点的三角形相似?若存在,求出相似比;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com