某商业公司为指导某种应季商品的生产和销售，对三月份至七月份该商品的售价和生产进行了调研，结果如下：一件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图A)；一件商品的成本Q(元)与时间t(月)的关系可用一条抛物线上的点来表示，其中6月份成本最高(如图B)．

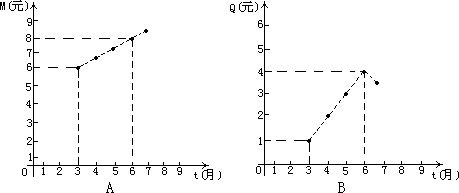
根据图像提供的信息解答下面问题：

(1)一件商品在3月份出售时的利润是多少元？(利润＝售价－成本)

(2)求图B中表示的一件商品的成本Q(元)与时间t(月)之间的函数关系式；

(3)你能求出三月份至七月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗？若该公司能在一个月内售出此种商品30000件，请你计算一下该公司在一个月内最少获利多少元？

阅读以下材料并完成后面的问题．

将直线y＝2x－3向右平移3个单位，再向上平移1个单位，求平移后的直线的解析式．

解：在直线y＝2x－3上任取两点A(1，－1)、B(0，－3)．

由题意知：

点A向右平移3个单位得(4，－1)；再向上平移1个单位得(4，0)．

点B向右平移3个单位得(3，－3)；再向上平移1个单位得(3，－2)．

设平移后的直线的解析式为y＝kx＋b．

则点(4，0)、(3，－2)在该直线上，

可解得k＝2，b＝－8．

所以平移后的直线的解析式为y＝2x－8．

根据以上信息解答下面问题：

将二次函数y＝－x²＋2x＋3的图像向左平移1个单位，再向下平移2个单位，求平移后的抛物线的解析式．(平移后抛物线形状不变)

如图，在等腰梯形AB∥⊥CD中，BC∥AD，BC＝8，AD＝20，AB＝DC＝10，点P从A点出发沿AD边向点D移动，点Q自A点出发沿A→B→C的路线移动，且PQ∥DC，若AP＝x，梯形位于线段PQ右侧部分的面积为S．

(1)分别求出当点Q位于AB、BC上时，S与x之间的函数关系式，并写出自变量x的取值范围；

(2)当线段PQ将梯形AB∥⊥CD分成面积相等的两部分时，x的值是多少？

(3)当(2)的条件下，设线段PQ与梯形AB∥⊥CD的中位线EF交于O点，那么OE与OF的长度有什么关系？借助备用图说明理由；并进一步探究：对任何一个梯形，当一直线l经过梯形中位线的中点并满足什么条件时，一定能平分梯形的面积？(只要求说出条件，不需要证明)

如图，AB是⊙O的直径，点P在AB的延长线上，弦CE交AB于点D，连结OE、AC，已知∠POE＝2∠CAB，∠P＝∠E．

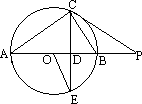
(1)求证：CE⊥AB；

(2)求证：PC是⊙O的切线；

(3)若BD＝2OD，且PB＝9，求⊙O的半径及tan∠P的值．

某边防部接到情报，近海处有一可疑船只A正向公海方向行驶，边防部迅速派出快艇B追赶．在追赶过程中，设快艇B相对于海岸的距离为y₁(海里)，可疑船只A相对于海岸的距离为y₂(海里)，追赶时间为t(分钟)，图中l_A、l_B分别表示y₂、y₁与t之间的关系．结合图象回答下列问题：

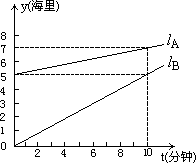
(1)请你根据图中标注的数据，分别求出y₁、y₂与t之间的函数关系式，并写出自变量的取值范围；

(2)15分钟内B能否追上A？说明理由；

(3)已知当A逃到离海岸12海里的公海时，B将无法对其进行检查．照此速度计算，B能否在A逃入公海前将其拦截？

在直角坐标系xOy中，O为坐标原点，A，B，C三点的坐标分别为A(5，0)，B(0，4)，C(－1，O)．点M和点N在x轴上(点M在点N的左边)，点N在原点的右边，作MP⊥BN，垂足为P(点P在线段BN上，且点P与点B不重合)，直线MP与y轴交于点G．MG＝BN．

(1)求经过A，B，C三点的抛物线的解析式；

(2)求点M的坐标；

(3)设ON＝t，△MOG的面积为s，求s与t的函数关系式，并写出自变量t的取值范围；

(4)这点B作直线BK平行于x轴，在直线BK上是否存在点R，使△ORA为等腰三角形，若存在，请直接写出点R的坐标，若不存在，请说明理由．

心理学家研究发现，一般情况下，学生的注意力随着教师讲课时间的变化而变化，讲课开始时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力y随时间t的变化规律有如下关系式：

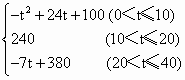
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较，何时学生的注意力更集中？

(2)讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？

(3)一道数学难题，需要讲解24分钟，为了效果较好，要求学生的注意力最低达到180，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？

(1)在2004年6月的日历中(见下左图)，任意图出一竖列上相邻的三个数，设中间的一个为a，则用含a的代数式表示这三个数(从小到大排列)分别是________．

(2)现将连续自然数1至2004按图中的方式排成一个长方形阵列，用一个正方形框出16个数(如上右图)．

①图中框出的这16个数的和是________；

②在上右图中，要使一个正方形框出的16个数之和分别等于2000，2004，是否可能？若不可能，试说明理由，若有可能，请求出该正方形框出的16个数中的最小数和最大数．

如图，在矩形ABCD中，AB＝3，AD＝2，点E、F分别在AB、DC上，AE＝DF＝2．现把一块直径为2的量角器(圆心为O)放置在图形上，使其线MN与EF重合；若将量角器线上的端点N固定在点F上，再把量角器绕点F顺时针方向旋转∠α(＜α＜)，此时量角器的半圆弧与EF相交于点P，设点P处量角器的读数为．

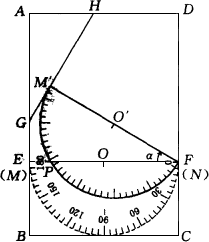
(1)用含的代数式表示∠α的大小；

(2)当等于多少时，线段PC与平行？

(3)在量角器的旋转过程中，过点作GH⊥，交AE于点G，交AD于点H．设GE＝x，△AGH的面积为S．试求出S关于x的函数关系式，并写出自变量x的取值范围．

在平面直角坐标系中，给定以下五点A(－2，0)，B(1，0)，C(4，0)，D(－2，)，E(0，－6)，从这五点中取三点，使经过这三点的抛物线满足以平行于y轴的直线为对称轴．我们约定：把经过三点A、E、B的抛物线表示为抛物线AEB(如图所示)．

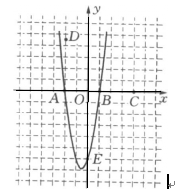
(1)问符合条件的抛物线还有哪几条？不求解析式，请用约定的方法一一表示出来；

(2)在(1)中是否存在这样的一条抛物线，它与余下的两点所确定的直线不相交？如果存在，试求出抛物线及直线的解析式；如果不存在，请说明理由．