有一只小昆虫落在数轴上的某点处，第一次它从向右爬1个单位到，第二次由向左爬2个单位到，第三次由向右爬3个单位到，第四次由向左爬4个单位到，…，按这样的规律它一共爬了1000次，最后停在点处，已知点表示的数是2004，请你求出这只小昆虫的起点所表示的数．

(2007，宁夏回族自治区，25)现代家居设计的“推拉式”钢窗，运用了轨道滑行技术，纱窗装卸时利用了平行四边形的不稳定性，操作步骤如下：

(1)将矩形纱窗转化成平行四边形纱窗后，纱窗上边框嵌入窗框的上轨道槽(如图1所示)

(2)将平行四边形纱窗的下边框对准窗框的下轨道槽(如图2)．

(3)将平行四边形纱窗还原成矩形纱窗，同时下边框嵌入窗框的下轨道槽(如图3)．

在装卸纱窗的过程中，如图所示的∠α的值不得小于81°，否则纱窗受损．现将高96cm的矩形纱窗恰好安装在上、下槽深分别为0.9cm，高96cm(上、下槽底间的距离)的窗框上．试求合理安装纱窗时∠α的最大整数值．(下表提供的数据可供使用)

(2005　辽宁十一市)如图所示，Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片，点O与原点重合，点A在x轴上，点C在y轴上，，∠CAO=30°．将Rt△OAC折叠，使OC边落在AC边上，点O与点D重合，折痕为CE．

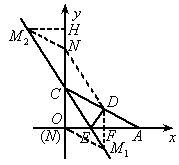
(1)求折痕CE所在直线的解析式；

(2)求点D的坐标；

(3)设点M为直线CE上的一点，过点M作AC的平行线，交y轴于点N，是否存在这样的点M，使得以M、N、D、C为顶点的四形边是平行四边形？若存在，请求出符合条件的点M的坐标；若不存在，请说明理由．

(2005　广东)如图所示，为测量小河的宽度，先在河岸边任意取一点A，再在河的另一边取两点B、C，测得∠ABC=45°，∠ACB=30°，量得BC长为20m．

(1)求小河的宽度(使用计算器的地区，结果保留三位有效数字；不使用计算器的地区，结果保留根号)；

(2)请再设计一种测量河宽度的方案，画出设计草图并作简要说明．

(2003　黑龙江)为美化环境，计划在某小区内用的草皮铺设一块边长为10m的等腰三角形绿地，请你求出这个等腰三角形绿地的另两边长．

(2005·烟台)(1)如图a所示，以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG，连接EG，试判断△ABC与△AEG面积之间的关系，并说明理由．

(2)园林小路，曲径通幽，如图b所示，小路由白色的正方形大理石和黑色的三角形大理石铺成．已知中间所有正方形的面积之和是，内圈所有三角形的面积之和是，这条小路一共占地多少平方米？

(2005　安徽芜湖)小胖和小瘦去公园玩标准的跷跷板游戏如图所示．两同学越玩越开心，小胖对小瘦说：“真可惜！我现在只能将你最高翘1m高，如果我俩各边的跷跷板都再伸长相同的一段长度，那么我就能将你翘到1.25m，甚至更高！”

(1)你认为小胖的话对吗？请你作图分析说明；

(2)你能否找出将小瘦翘到1.25m高的方法？试说明．

(2005　湖南长沙)已知点E、F在△ABC的边AB所在的直线上，且AE=BF，FH∥EG∥AC，FH、EG分别交边BC所在的直线于点H、G．

(1)如图所示，如果点E、F在边AB上，那么EG＋FH=AC；

(2)如图所示，如果点E在边AB上，点F在AB的延长线上，那么线段EG、FH、AC的长度关系是________；

(3)如图，如果点E在AB的反向延长线上，点F在AB的延长线上，那么线段EG、FH、AC的长度关系是________．

对(1)、(2)、(3)三种情况的结论，请任选一个给予证明，

(2003　浙江绍兴)已知∠AOB=90°，OM是∠AOB的平分线，按以下要求解答问题：

(1)将三角形的直角顶点P在射线OM上移动，两直角边分别与边OA、OB交于点C、D．

①在图中，证明：PC=PD；

②在图中，点G是CD与OP的交点，且PD，求△POD与△PDG的面积之比．

(2)将三角板的直角顶点P在射线OM上移动，一直角边与边OB交于点D，OD=1，另一直角边与直线OA、直线OB分别交于点C、E，使以P、D、E为顶点的三角形与△OCD相似，在图中作出图形，试求OP的长．

(2005　广西桂林)已知∠MON=90°，等边三角形ABC的一个顶点A是射线OM上的一定点，顶点B与点O重合，顶点C在∠MON内部．

(1)当顶点B在射线ON上移动到时，连接，请在∠MON内部作出以为一边的等边三角形(保留作图痕迹，不写作法和证明)；

(2)设与OC交于点Q，AC的延长线与交于点D．求证：；

(3)连接，试猜想为多少度？并证明你的猜想．