已知：如图所示，⊙O和⊙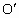相交于A、B两点，AC是⊙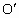的切线，交⊙O于点C，连结CB并延长交⊙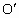于点F，D为⊙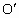上的点，且∠DAB＝∠C，连结DB并延长交⊙O于点E．

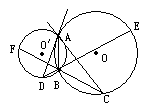
(1)求证：DA是⊙O的切线；

(2)求证：AC²∶AD²=BC∶BD；

(3)若BF=4，CA=3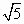，求DE的长

如图所示，已知PA切⊙O于点A，割线PBC交⊙O于B、C，PD⊥AB于D，PD、AO的延长线交于点E，连结CE并延长交⊙O于点F，连结AF．

(1)求证：△PBD∽△PEC；

(2)若AB＝12，tan∠EAF=，求⊙O的半径的长．

 如图所示，已知：抛物线y＝ax²＋bx与x轴的一个交点为B，顶点A在直线y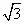＝x上，O为坐标原点．

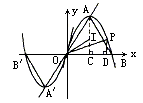
(1)证明：△OAB为等边三角形；

(2)若△OAB的内切圆半径为1，求出抛物线的解析式；

(3)在抛物线上是否存在点P，使△POB是直角三角形？若存在，请写出点P的坐标；若不存在，请说明理由．

如图所示，已知：直线y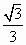＝x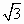＋与x轴、y轴分别交于A、B两点，⊙M经过原点O及A、B两点．

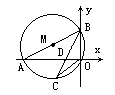
(1)求以OA、OB两线段长为根的一元二次方程；

(2)C是⊙M上一点，连结BC交OA于点D，若∠COD＝∠CBO，写出经过O、C、A三点的二次函数的解析式；

(3)若延长BC到E，使DE＝2，连结EA，试判断直线EA与⊙M的位置关系，并说明理由．

通过电脑拨号上“因特网”的费用是由电话费和上网费两部分组成．以前我市通过“黄冈热线”上“因特网”的费用为电话费0.18元/3min，上网费为7.2元/h．后根据信息产业部调整“因特网”资费的要求，自1999年3月1日起，我市上“因特网”的费用调为电话费0.22元/3min．上网费为每月不超过60h，按4元/h计算；超过60h部分，按8元/h计算．

(1)根据调整后的规定，将每月上“因特网”的费用y(元)表示为上网时间x(h)的函数；

(2)资费调整前，网民晓刚在其家庭经济预算中，一直有一笔每月70h的上网费用支出．“因特网”资费调整后，晓刚要想不超过其家庭经济预算中的上网费用支出，他现在每月至多可上网多少小时？

(3)从资费调整前后的角度分析，比较我市网民上网费用的支出情况．

如图所示，已知直线y＝－2x＋12分别与y轴、x轴交于A、B两点，点M在y轴上，以点M为圆心的⊙M与直线AB相切于点D，连结MD．

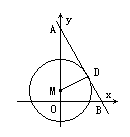
(1)求证：△ADM∽△AOB；

(2)如果⊙M的半径为2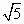，请求出点M的坐标，并求出以(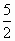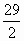－，)为顶点，且过点M的抛物线的解析式；

(3)在(2)的条件下，试问：在此抛物线上是否存在点P，使得以P、A、M三点为顶点的三角形与△AOB相似？如果存在，请求出所有符合条件的点P的坐标；如果不存在，请说明理由．

如图所示，已知：⊙P与x轴相切于坐标原点O，点A(0，2)是⊙P与y轴的交点，点B(－2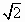，0)在x轴上，连结BP交⊙P于点C，连结AC并延长交x轴于点D．

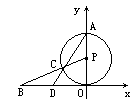
(1)求线段BC的长；

(2)求直线AC的函数解析式；

(3)当点B在x轴上移动时，是否存在点B，使△BOP相似于△AOD？若存在，求出符合条件的点的坐标；若不存在，说明理由．

如图所示，已知：抛物线c₁经过A、B、C三点，顶点为D，且与x轴的另一个交点为E．

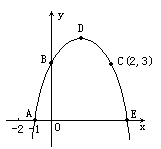
(1)求抛物线c₁的解析式．

(2)求四边形ABDE的面积．

(3)△AOB与△BDE是否相似？如果相似，请予以证明；如果不相似，请说明理由．

(4)设抛物线c₁的对称轴与x轴交于点F；另一条抛物线c₂经过点E(抛物线c₂与抛物线c₁不重合)，且顶点为M(a，b)，对称轴与x轴相交于点G，且以M、G、E为顶点的三角形与以D、E、F为顶点的三角形全等．求a、b的值(只写出结果，不必写出解答过程)．