
科目: 来源: 题型:047
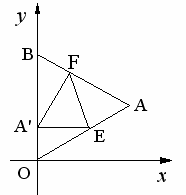
如图,△OAB是边长为![]() 的等边三角形,其中O是坐标原点,顶点B在
的等边三角形,其中O是坐标原点,顶点B在![]() 轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.
轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E//![]() 轴时,求点A′和E的坐标;
轴时,求点A′和E的坐标;
(2)当A′E//![]() 轴,且抛物线
轴,且抛物线![]() 经过点A′和E时,求抛物线与
经过点A′和E时,求抛物线与![]() 轴的交点的坐标;
轴的交点的坐标;
(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.
查看答案和解析>>
科目: 来源:素质教育新学案·初中几何·第三册 题型:047
如图所示,已知⊙![]() 与⊙
与⊙![]() 外切于F点,DE为公切线,过F点的直线交⊙
外切于F点,DE为公切线,过F点的直线交⊙![]() 于点A,交⊙
于点A,交⊙![]() 于点B,BE、AD的延长线交于C点,求证AC⊥BC.
于点B,BE、AD的延长线交于C点,求证AC⊥BC.

查看答案和解析>>
科目: 来源: 题型:047
如图所示,△DEF中,DE=DF,过EF上一点A作直线与DE交于点B、与DF的延长线交于点C,且BE=CF.
求证:AB=AC.
证明:过B作BG∥CD交EF于G,∴∠EGB=∠EFD.∵DE=DF,∴_________.

∴__________.∴BE=BG.
∵BE=CF,∴BG=CF.
∵BG∥CD,∴∠GBA=∠FCA,∠AGB=∠AFC.
∴△AGB≌△AFC.∴AB=AC.
阅读后回答下列问题:
(1)
试在上述过程中的横线上填写适当的步骤.(2)
还有别的辅助线作法吗?若有,试说出一种:______________.(3)
若DE=DF,AB=AC,则BE、CF之间有何关系?(4)
若AB=AC,BE=CF,DF=8cm,则DE的长为__________.(5)
若AB=m·AC,DE=DF,CF=a,则BE的长为__________.查看答案和解析>>
科目: 来源: 题型:047
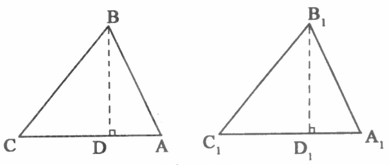
我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1Cl,∠C=∠Cl.
求证:△ABC≌△A1B1C1.
(请你将下列证明过程补充完整.)
证明:分别过点B,B1作BD⊥CA于D,B1 D1⊥C1 A1于D1.
则∠BDC=∠B1D1C1=900,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,-
∴BD=B1D1.
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com