如图，BC为⊙O的直径，AD上BC于点D，点P为弧AC上一动点，连接PB，分别交AD，AC于点E，F．

(1)当＝时，求证AE＝BE；

(2)当点P在什么位置时，AF＝EF？

如图，AB是⊙O的直径．

(1)操作：在⊙O上任取一点C(不与A，B重合)，过点C作⊙O的切线；过点A作过点C的切线的垂线AD，垂足为D，交BC的延长线于点E．

(2)根据上述操作及已知条件，在图中找出一些相等的线段，并证明你所得到的结论．

如图，半径不等的⊙O₁，⊙O₂外离，线段O₁O₂分别交⊙O₁，⊙O₂于点A，B，MN为两圆的公切线，分别切⊙O₁，⊙O₂于点M，N，连接MA，NB．请判断∠AMN与∠BNM的大小关系，并证明你的结论．

命题：如图，在锐角△ABC中，BC＝a，CA＝b，AB＝c，△ABC的外接圆半径为R，则＝2R．

证明：连接CO并延长交⊙O于点D，连接DB，则∠D＝∠A．

∵CD为⊙O的直径，∴∠DBC＝90°．

在Rt△DBC中，∵sinD＝＝，∴sinA＝，即＝2R．

同理＝2R，＝2R．

∴＝2R．

请你阅读前面所给的命题及其证明后，完成下面的(1)(2)两小题：

(1)前面的阅读材料中略去了“＝2R和＝2R”的证明过程，请你把“＝2R”的证明过程补写出来．

(2)直接用前面阅读材料中命题的结论解题．

已知：如图，在锐角△ABC中，BC＝，CA＝，∠A＝60°．求△ABC的外接圆半径R及∠C．

如图，AB是⊙O的直径，C为⊙O上的一点，AD和过点C的切线相交于D，和⊙O相交于E，如果AC平分∠DAB，求证∠ADC＝90°．

如图，AB是⊙O 的直径，直线MN 交⊙O于C、D 两点，AE⊥MN，BF⊥MN，垂足分别为E，F．

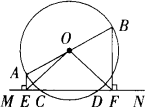
(1)求证CE＝DF，OE＝OF；

(2)当MN向上平移与AB相交时，如果其他条件不变，(1)中的结论是否仍然成立？

如图，在⊙O中，已知AB为直径，C，D为⊙O上的两点，且C，D在AB的两侧，OD⊥AB，求证DC平分∠ACB．

如图，已知AB为⊙O的直径，半径OC⊥AB，E为OB上一点，弦AD⊥CE交OC于点F，求证OE＝OF．

如图，等腰梯形ABCD中，AD∥BC，点E是线段AD上的一个动点(E与A、D不重合)，G、F、H分别是BE、BC、CE的中点．

(1)试探索四边形EGFH的形状，并说明理由．

(2)当点E运动到什么位置时，四边形EGFH是菱形？并加以证明．

(3)若(2)中的菱形EGFH是正方形，请探索线段EF与线段BC的关系，并证明你的结论．

如图，先把一矩形ABCD纸片对折，设折痕为MN，再把B点叠在折痕线上，得到△ABE．过B点折纸片使D点叠在直线AD上，得折痕PQ．

(1)求证：△PBE∽△QAB；

(2)你认为△PBE和△BAE相似吗？如果相似给出证明，如补相似请说明理由；

(3)如果直线EB折叠纸片，点A是否能叠在直线EC上？为什么？