
科目: 来源:中学教材全解 七年级数学下 (北京师大版) 北京师大版 题型:044
如图,四张纸片上的三角形中有三个完全相同的直角三角形,另一个也有一边与这个直角三角形的斜边相等,把这四张纸片放在盒子里搅匀,然后随机地取两张,这两张图形:

(1)能拼成矩形的机会有多大?(2)能拼成平行四边形的机会有多大?(3)能拼成等腰三角形的机会有多大?(4)只能拼成一般四边形的机会有多大?
查看答案和解析>>
科目: 来源:中学教材全解 七年级数学下 (北京师大版) 北京师大版 题型:044
某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图所示),并规定:顾客每购买100元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元,50元,20元的购物券(转盘等分成20份).
问:甲顾客购物120元,他获得购物券的概率是多少?他得到100元,50元,20元购物券的概率分别是多少?

查看答案和解析>>
科目: 来源:中学教材全解 七年级数学下 (北京师大版) 北京师大版 题型:044
如图是由转盘和箭头组成的两个装置,装置A、B的转盘分别被分成三个面积相等的扇形,装置A上的数字分别是1,6,8,装置B上的数字分别是4,5,7,这两个装置除了表面数字不同外,其他的构造完全相同.现在你和另外一个人分别同时用力转动A、B两个转盘中的箭头,如果我们规定箭头停留在较大数字的一方获胜(若箭头恰好停留在分界线上,则重新转动一次,直到箭头停留在某一数字为止),那么你会选择哪个装置呢?请借助列表法或树状图法说明理由.

查看答案和解析>>
科目: 来源:中学教材全解 七年级数学下 (北京师大版) 北京师大版 题型:044
“抛阶砖”是游戏场的典型游戏之一.如图(1),参与者只需将手上的“金币”抛落身边若干距离的阶砖平面上,抛出的硬币刚巧落在任何一个阶砖的范围内(不与阶砖相连的线重叠),便可获奖.要注意“金币”与阶砖的相对大小将会决定成功抛中阶砖的机会.由于阶砖是正方形,可设每边长度为a,金币的直径为d.若“金币”成功落在阶砖上,它的圆心必位于图(2)的阴影部分内,即“成功”部分是边长为(a-d)的正方形.
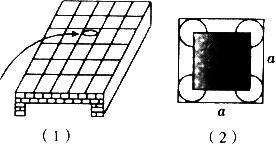
(1)计算“金币”抛落在阶砖范围内的概率(用含a、d的式子表示,0<d<a);
(2)通过配搭“金币”与阶砖之间的大小的设计,做这个“抛阶砖”的游戏,并作好记录,你发现什么规律?
查看答案和解析>>
科目: 来源:中学教材全解 七年级数学下 (北京师大版) 北京师大版 题型:044
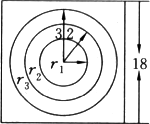
某馅饼店设有一个投镖靶,如图该靶为正方形板,边长为18厘米,挂于大门附近的墙上.顾客花伍角硬币便可投一镖,并有机会赢得三种意大利馅饼中的一个.投镖靶中画有三个同心圆,圆心在靶的中心,当投镖击中半径为1厘米的最内层圆形区域时,可得到一个大馅饼;当投镖击中半径为1厘米到2厘米之间的环形区域时,可得到一个中馅饼;当投镖击中半径为2厘米到3厘米之间的环形区域时,可得到一个小馅饼;如果击中靶上的其他部分,则得不到馅饼.我们假设每一个顾客都能投镖中靶,并假设每个圆的周边线没有宽度,即每次投镖不会击中线上,试求一顾客将赢得:(1)一张大馅饼的概率;(2)一张中馅饼的概率;(3)一张小馅饼的概率;(4)没得到馅饼的概率.
查看答案和解析>>
科目: 来源:中学教材全解 七年级数学下 (北京师大版) 北京师大版 题型:044
如图是两个可以自由转动的转盘,转盘被等分成若干个扇形.请你利用上面两个转盘设计如下游戏:

(1)使概率等于![]() ;(2)使概率等于
;(2)使概率等于![]() ;(3)设计最大概率的游戏.
;(3)设计最大概率的游戏.
查看答案和解析>>
科目: 来源:中学教材全解 七年级数学下 (北京师大版) 北京师大版 题型:044
(趣味题)小明有三双颜色不同的鞋,分别为红、黄、白,随便穿一只在左脚,再随便找一只穿右脚,正好是一双的可能性为多少?
查看答案和解析>>
科目: 来源:中学教材全解 七年级数学下 (北京师大版) 北京师大版 题型:044
(开放题)如图所示,转盘被分成16个相等的扇形,请在转盘适当地方涂上颜色,使得自由转动这个转盘,当它停止转动时,指针落在红色区域的概率为![]() ,你还能举出一个不确定事件,它发生的概率也是
,你还能举出一个不确定事件,它发生的概率也是![]() 吗?
吗?

查看答案和解析>>
科目: 来源:中学教材全解 七年级数学下 (北京师大版) 北京师大版 题型:044
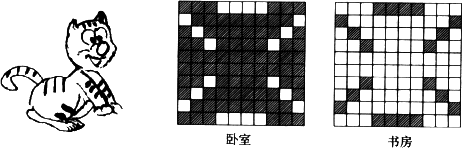
如图是卧室和书房地板的示意图,图中每一地砖除颜色外完全相同,小猫分别在卧室和书房中自由地走来走去,在哪个房间里,小猫停留在黑砖上的概率大?
查看答案和解析>>
科目: 来源:中学教材全解 七年级数学下 (北京师大版) 北京师大版 题型:044
小明的爸爸在午饭过后,突然心血来潮,欲前往投注站买六合彩.小明却从裤袋里拿出一枚硬币,一脸认真地对爸爸说:“你真的甘愿把钱投注在一个中奖机会近似为零的游戏中吗?不如你试用这个硬币去测试一下今天的运气吧.
如果连续24次掷得硬币的同一面(正面或背面皆可)朝上,你再去投注也未迟呢!”
拿过小明的硬币投掷数次后,爸爸说:“不可能都同一面朝上,这与买彩票有什么关系?我还是去买彩票.”小明说:“这里面有科学道理,可以让我给你算一算中奖的机会有多大,之后,你再去买也不迟.”
小明利用了概率计算的乘法定律:若P1和P2分别为事件E1和E2出现的概率,则E1和E2同时出现的概率或E2跟随E1出现的概率为P1×P2.这一种运算方式可推广到n个事件出现的情况.
小明拿出纸与计算器,把六合彩中一等奖、二等奖、三等奖的概率逐一进行下面的运算:
中一等奖者,需从47个号码中选中6个与开采出来相同的号码;二等奖则须中5个号码和1个特别号码;若只中5个号码,便会得三等奖.基于这些中奖的条件,小明利用概率的乘法定律计算出以下的概率.
中一等奖的概率=![]() =0.000 000 09(精确至8位小数).
=0.000 000 09(精确至8位小数).
中二等奖的概率=![]() =0.000 000 6(精确至7位小数).
=0.000 000 6(精确至7位小数).
中三等奖的概率=![]() =0.000 02(精确至5位小数).
=0.000 02(精确至5位小数).
计算后,小明说中六合彩的机会可以说近似为0,爸爸说:“你为什么让我连续掷硬币呢?它与中六合彩有联系吗?”小明告诉爸爸连续24次掷硬币且同一面朝上的概率为![]() 是一个近似于零的数与中六合彩的概率可以相比.看了小明的计算,爸爸打消了买六合彩中奖的念头.
是一个近似于零的数与中六合彩的概率可以相比.看了小明的计算,爸爸打消了买六合彩中奖的念头.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com