
科目: 来源:双色笔记九年级数学(上) 题型:044
已知:如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a.
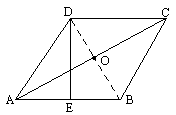
求:(1)∠ABC的度数;(2)对角线AC的长;(3)菱形ABCD的面积.
查看答案和解析>>
科目: 来源:双色笔记九年级数学(上) 题型:044
如图,在平行四边形ABCD中,AQ、BN、CN、DQ分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN交于P,CN与DQ交于M,在不添加其他条件的情况下,试写出一个由上述条件推出的结论,并给出证明过程.
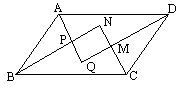
(要求:推理过程要用到“平行四边形”和“角平分线”这两个条件)
查看答案和解析>>
科目: 来源:双色笔记九年级数学(上) 题型:044
阅读与思考:
(1)下面是课本中对平行四边形判定定理4(一组对边平行且相等的四边形是平行四边形)的证明,请边阅读,边进行推理填空,然后思考后面的问题.
已知:如图在四边形ABCD中,AB∥CD,且AB=CD.

求证:四边形ABCD是平行四边形.
证明:连结AC.
∵AB∥CD( ),
∴∠1=∠2( ),
又∵AB=CD( ),AC=AC( ),
∴△ABC≌△CDA( ),
∴BC=AD,∴四边形ABCD是平行四边形( )上面的证明是利用平行四边形判定定理________完成的.在证明过程中,证明了△ABC≌△CDA,由此还可以推出∠B=________,同理可证∠A=________,可见,平行四边形判定定理4也可以利用平行四边形判定定理________来证明.在图中再连结BD,设AC与BD相交于点O,则可以利用判定三角形全等的________公理证明△AOB≌△________,进而推出AO=________,BO=________,这说明平行四边形判定定理4也可以利用平行四边形判定定理________来证明.
(2)如果要画平行四边形ABCD,使∠B=![]() ,AB=2cm,BC=3cm,请回答下列问题:
,AB=2cm,BC=3cm,请回答下列问题:
①利用平行四边形判定定理2画所求的平行四边形ABCD,在画出AB、BC后,怎样确定点D的位置?
②利用平行四边形判定定理3画所求的平行四边形ABCD,应按怎样的步骤进行?请写出画法.
③利用平行四边形判定定理4画所求的平行四边形ABCD,在画出AB、BC后,怎样确定点D的位置?
查看答案和解析>>
科目: 来源:双色笔记九年级数学(上) 题型:044
如图,在河L1、L2外侧有A、B两个城镇,现计划架设两道桥EF和CD(设L1、L2河两岸互相平行).求A镇到B镇的最近距离(注:桥应和岸垂直).
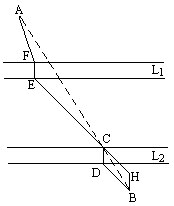
设计方案如下:
(1)确定C点,使C为直线AB与L2河岸的交点;
(2)作CD⊥L2的另一河岸于D,连结BD,作BH∥CD,作CH∥BD,其交点为H;
(3)延长HC交L1河岸于E,作EF⊥L1交另一河岸于F,连结AF.
试问:从A→F→E→C→D→B的距离是否最短?依据是什么?
查看答案和解析>>
科目: 来源:双色笔记九年级数学(上) 题型:044
如图,田村有一口呈四边形的池塘,在它的四个角A、B、C、D处均种有一棵大核桃树.田村准备开挖池塘建养鱼池,想使池塘的面积扩大一倍,又想保持核桃树不动,并要求扩建后的池塘成平行四边形形状,请问田村能否实现这一设想?若能,请你设计并画出图形;若不能,请你说明理由(画图要保留痕迹,不写做法).
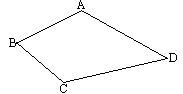
查看答案和解析>>
科目: 来源:双色笔记八年级数学上(北京师大版) 题型:044
在平面直角坐标系中,将坐标为(2,0),(2,2),(0,2),(0,3),(2,5),(3,5),(2,2),(5,3),(5,2),(3,0),(2,0),(4,4)的点用线段一次连接起来形成一个图案.
(1)每个点的横坐标保持不变,纵坐标变为原来的![]() ,再将所得的各点用线段依次连接起来,所得图案与原图案相比有什么变化?
,再将所得的各点用线段依次连接起来,所得图案与原图案相比有什么变化?
(2)纵坐标保持不变,横坐标分别加3呢?
(3)横坐标保持不变,纵坐标分别加3呢?
(4)纵坐标保持不变,横坐标分别乘-1呢?
(5)横坐标保持不变,纵坐标分别乘-1呢?
(6)横、纵坐标分别变成原来的2倍呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com