心理学家发现，学生对概念的接受能力y与提出概念所用的时间x(单位：分钟)之间满足函数关系：y＝－0.1x²＋2.6x＋43(0≤x≤30)．y值越大，表示接受能力越强．

(1)x在什么范围内，学生的接受能力逐步增强？x在什么范围内，学生的接受能力逐步降低？

(2)第10分钟时，学生的接受能力是多少？

(3)第几分钟时，学生的接受能力最强？

某商场销售一批衬衫，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经过市场调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．

(1)若商场平均每天要盈利1 200元，每件衬衫应降价多少元？

(2)每件衬衫降价多少元时，商场平均每天盈利最多？

如图，有长为24 m的篱笆，一面利用墙(墙的最大可用长度a为10 m)，围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x m，面积为S m²．

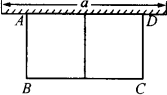
(1)求S与x的函数关系式；

(2)如果要围成面积为45 m²的花圃，AB的长是多少米？

(3)能围成面积比45 m²更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由．

画图求方程x²＝－x＋2的解，你是如何解决的呢？我们来看一看两位同学不同的方法．

甲：将方程x²＝－x＋2化为x²＋x－2＝0，画出y＝x²＋x－2的图象，观察它与x轴的交点，得出方程的解．

乙：分别画出函数y＝x²和y＝－x＋2的图象，观察它们的交点，把交点的横坐标作为方程的解．

你对这两种解法有什么看法？请与你的同学交流．

已知二次函数y＝x²＋ax＋a－2．

(1)说明抛物线y＝x²＋ax＋a－2与x轴有两个不同交点；

(2)求这两个交点间的距离(关于a的表达式)；

(3)a取何值时，两点间的距离最小？

已知二次函数y＝－x²＋(m－2)x＋m＋1．

(1)试说明：不论m取任何实数，这个二次函数的图象必与x轴有两个交点；

(2)m为何值时，这两个交点都在原点的左侧？

(3)m为何值时，这个二次函数的图象的对称轴是y轴？

已知下表：

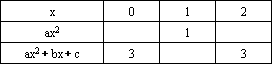
(1)求a、b、c的值，并在表内空格处填入正确的数；

(2)请你根据上面的结果判断：

①是否存在实数x，使二次三项式ax²＋bx＋c的值为0？若存在，求出这个实数值；若不存在，请说明理由．

②画出函数y＝ax²＋bx＋c的图象示意图，由图象确定，当x取什么实数时，ax²＋bx＋c＞0．

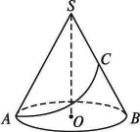
已知圆锥底面直径AB＝20，母线SA＝30，C为母线SB的中点．今有一小虫沿圆锥侧面从A点爬到C点觅食(如图)，问它爬过的最短距离应是多少？

如图，已知圆锥的母线长AB＝6 cm，

底面半径OB＝2 cm．

求：(1)圆锥的高AO；

(2)锥角∠CAB的正切值．

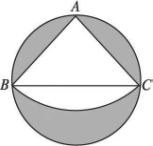
如图，有一直径是1米的圆形铁皮，要从中剪出一个最大的圆心角是90度的扇形ABC，求：(1)被剪掉阴影部分的面积；(2)用所留的扇形铁皮围成一个圆锥，该圆锥的底面半径是多少？