
科目: 来源: 题型:044
一个有进水管与出水管的容器,单位时间内进出的水量都是一定的,设从某时刻开始的4分内只进水不出水,在随后的8分内既进水又出水,容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.
(1)求0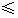 x
x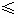 4时y随x变化的函数关系式.
4时y随x变化的函数关系式.
(2)求4<x 12时y随x变化的函数关系式.
12时y随x变化的函数关系式.
(3)每分钟进水、出水各多少升?
查看答案和解析>>
科目: 来源: 题型:044
已知一次函数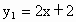 和
和 ,画函数图象回答下列问题.
,画函数图象回答下列问题.
(1)求方程-2x+2=0的解;
(2)求不等式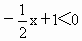 的解集;
的解集;
(3)求方程组 的解;
的解;
(4)当x为何值时,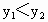 ;
;
(5)当x为何值时,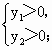
(6)当x为何值时,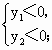
(7)在-1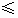 x
x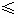 2范围内,求
2范围内,求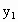 ,
,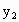 的最大或最小值.
的最大或最小值.
画函数图象
查看答案和解析>>
科目: 来源: 题型:044
某公司到果园基地购买某种优质水果用来慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案是每千克9元,由基地送货上门;乙方案是每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果量x(千克)之间的函数关系式,并写出自变量x的取值范围;
(2)当购买量在什么范围时,选择哪种购买方案付款最少?并说明理由.
查看答案和解析>>
科目: 来源: 题型:044
为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台价格、月处理污水量及年消耗费如下表:
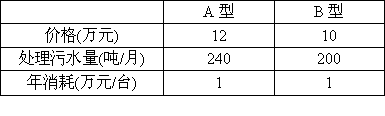
经预算该企业购买设备资金不高于105万元.
(1)请你计算该企业可以有几种购买方案?
(2)若企业每月生产的污水量为2040吨,为了节约资金,应选用哪种购买方案.
查看答案和解析>>
科目: 来源: 题型:044
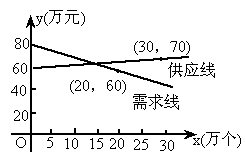
随着教学手段不断提高,要求计算器进入课堂,某电子厂家经市场调查,发现某种计算器的供应量x(万个)与价格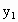 (万元)之间的关系如图中供应线表示,而需求量x(万个)与价格
(万元)之间的关系如图中供应线表示,而需求量x(万个)与价格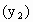 万元之间关系如图中需求线所示,如果你是这个电子厂厂长,应计划生产这种计算器多少个,每个销售多少元,才能使市场达到供需平衡?(结果保留一位小数)
万元之间关系如图中需求线所示,如果你是这个电子厂厂长,应计划生产这种计算器多少个,每个销售多少元,才能使市场达到供需平衡?(结果保留一位小数)
查看答案和解析>>
科目: 来源: 题型:044
A、B两地相距100千米,甲、乙两人骑车同时分别从A、B两地相向而行,假设他们都保持匀速行驶,则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数,1小时后,乙距离A地80千米,2小时后甲距离A地30千米,问经过多长时间两人将相遇?(结果用分数表示)
查看答案和解析>>
科目: 来源: 题型:044
A,B两地相距50km,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,如图折线PQR和线段MN分别表示甲和乙所行驶的里程S与该日下午时间t之间关系.
(1)甲出发多少小时,乙才开始出发?
(2)乙行驶多少小时就追上了甲,这时两人离B地还有多少千米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com