从分别标有数字1～5的五张卡片中，随意抽出两张，先估计下列事件发生的机会的大小，将他们按从小到大的顺序排成一列，再用逻辑分析的方法求出各个事件发生的概率，看看你的估计是否正确．

(1)抽出的两张卡片上的数字之和恰为奇数；

(2)抽出的两张卡片上的数字之和恰为偶数；

(3)抽出的两张卡片上的数字之和恰为4的倍数；

(4)抽出的两张卡片上的数字之和恰为小于12的数；

(5)抽出的两张卡片上的数字之和恰为大于12的数．

为了预防“非典”，某学校对教室采用药薰消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y(毫克)与时间x(分)成正比例．药物燃烧后，y与x成反比例，如图所示，现测得药物8分钟燃烧完毕．此时室内空气中每立方米的含药量为6毫克，请你根据题中所提供的信息，解答下列问题：

(1)药物燃烧时，y与x的函数关系式为________，自变量x的取值范围是________；

(2)药物燃烧后，y关于x的函数关系式为________；

(3)研究表明，当空气中的含药量低于1.6毫克时，学生方可进教室．那么从消毒开始，至少经过多少分钟，学生方可回到教室？

(4)研究表明，当空气中每立方米的含药量不低于1.6毫克且持续时间不低于10分钟时，方能有效杀死空气中的病菌，那么此次消毒是否有效？为什么？

如图所示，矩形ABCD中，AB＝10cm，BC＝20cm，P、Q两点同时从A点出发．分别以1厘米／秒和2厘米／秒的速度沿A→B→C→D→A运动，当Q点回到A点时，P、Q两点即停止运动，设P、Q运动时间为t秒．

(1)当P、Q分别在AB边和BC边上运动时，设以P、B、Q为顶点的三角形面积为S．请写出S关于t的函数解析式及自变量t的取值范围；

(2)在整个运动过程中，t取何值时，PQ与BD垂直．

一次函数y＝kx＋2与反比例函数y＝的图像交于A、B两点，A点纵坐标为－1，B点横坐标为2，求这两个函数解析式．

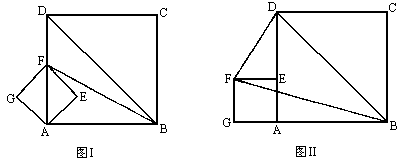
如图Ⅰ，四边形AEFG与ABCD都是正方形，它们的边长分别为a、b(b≥2a)，且点F在AD上．(以下问题的结果可用a、b的代数式表示)

(1)求S_△DBF；

(2)把正方形AEFG绕点A按逆时针方向旋转得图Ⅱ，求图中S_△DBF；

(3)把正方形AEFG绕点A旋转任意角度，在旋转过程中，S_△DBF是否存在最大值、最小值？如果存在，试求出最大值、最小值；若不存在，请说明理由．

读一读，想一想，做一做：

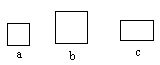
现有足够的2×2，3×3的正方形和2×3的矩形图片a、b、c(如图)，现各选若干个图片拼成不同的图形，请你在下面给出的方格纸中，按下列要求分别画一种拼法示意图(说明：下面给出的方格纸中，每个小正方形的边长均为1，拼出的图形要求每两个图片之间既无缝隙，也不重叠，画图必须保留拼图的痕迹)．

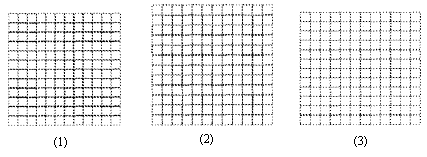
①选取a型、b型两种图片各1块、c型图片2块，在下面的图1中拼成一个正方形；

②选取a型图片4块、b型图片1块、c型图片4块，在下面的图(2)中拼成一个正方形．

③选取a型图片3块、b型图片1块，再选取若干c型图片，在下面图(3)中拼成一个矩形．

读一读，想一想，做一做：

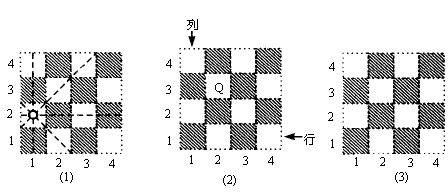
国际象棋、中国象棋和围棋号称为世界三大棋种．国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多：“皇后”不仅能控制她所在的行与列中的每一个小方格，而且还能控制“斜”方向的两直线上的每一个小方格，如图(1)是一个4×4的小方格棋盘，图中的“皇后Q”能控制图中虚线所经过的每一个小方格．

①在如图(2)的小方格棋盘中有一“皇后Q”，她所在的位置可用“(2，3)”来表示，请说明“皇后Q”所在的位置“(2，3)”的意义，并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置．

②如图(3)也是一个4×4的小方格棋盘，请在这个棋盘中放入四个“皇后Q”，使这四个“皇后Q”之间互相不受对方控制(在图丙中的某四个小方格中标出字母Q)即可．

解答题

如图，四边形ABCD中，AC＝6，BD＝8，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A₁B₁C₁D₁；再顺次连接四边形A₁B₁C₁D₁各边中点，得到四边形A₂B₂C₂D₂……如此进行下去得到四边形A_nB_nC_nD_n．

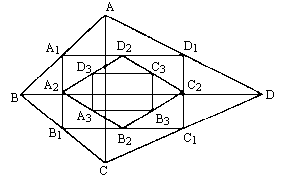
(1)证明：四边形A₁B₁C₁D₁是矩形；

(2)写出四边形A₁B₁C₁D₁和四边形A₂B₂C₂D₂的面积；

(3)写出四边形A_nB_nC_nD_n的面积；

(4)求四边形A₅B₅C₅D₅的周长．

如图，在平面直角坐标系内，点A与C的坐标分别为(4，8)、(0，5)．过点A作AB⊥x轴于点B，边OB上的动点D作直线y＝kx＋b平行于AC，与AB相交于点E连结CD，过点E作直线EF∥CD，交AC于点F．

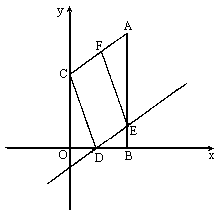
(1)求经过点A、C两点的直线的解析式．

(2)当点D在OB上移动时，能否使四边形CDEF成为矩形？若能，求出此时的k、b的值；若不能，请说明理由．

(3)如果将直线AC作向上平移，交y轴于点C，交AB于点，连结，过点E作∥．

交于点，那么能否使四边形成为正方形？若能，请求出此时正方形的面积；若不能，请说明理由．

如图，把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图①)，且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合，现将三角板EFG绕O点按顺时针方向旋转(旋转角α满足条件：＜α＜)，四边形CHGK是旋转过程中两三角板的重叠部分(如图②)．

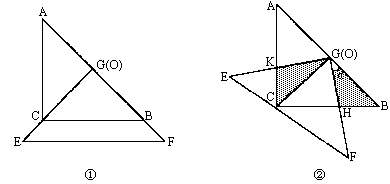
(1)在上述旋转过程中，BH与CK有怎样的数量关系？四边形CHGK的面积有何变化？证明你发现的结论；

(2)连接HK，在上述旋转过程中，设BH＝x，△GKH的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围；

(3)在(2)的前提下，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的？若存在求出此时x的值；若不存在，说明理由．