
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
(1)填表:

(2)已知一条抛物线的形状(开口方向和开口大小)与抛物线y=2x2的相同,它的对称轴是直线x=-2,且当x=1时,y=6,求这条抛物线的解析式.
(3)定义:如果点P(t,t)在抛物线上,则点P叫做这条抛物线的不动点.
①求出(2)中所求抛物线的所有不动点的坐标;
②当a,b,c满足什么关系式时,抛物线y=ax2+bx+c一定存在不动点?
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
由抛物线y=x2-2mx+m2+2m-1,①有y=(x-m)2+2m-1,②
∴抛物线的顶点坐标为(m,2m-1),即![]()
当m的值变化时,x,y的值也随之变化,同时y的值也随x的值的变化而变化,将③代入④,得y=2x-1.
可见,不论m取何实数,抛物线顶点的纵坐标y和横坐标x都满足关系式y=2x-1.回答下列问题.
(1)上述过程中,由①到②所用的数学方法是________,其中运用了________公式,由③④到⑤所用的数学方法是________;
(2)根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-3m+1的顶点的纵坐标y与横坐标x之间的关系式.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
已知直线y=![]() +3与抛物线y=-
+3与抛物线y=-![]() ,设直线与x轴、y轴分别交于A,B两点,今将抛物线作两次平移后,使之通过A,B两点,求平移后的抛物线的解析式及顶点坐标.
,设直线与x轴、y轴分别交于A,B两点,今将抛物线作两次平移后,使之通过A,B两点,求平移后的抛物线的解析式及顶点坐标.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如下图所示,已知抛物线y=ax2+bx+c经过A(-1,0),B(1,0),M(0,1)三点,直线l平行于x轴,且与抛物线交于C,D两点,连接DA,BC,若C点的横坐标是![]() ,求梯形ABCD的面积.
,求梯形ABCD的面积.
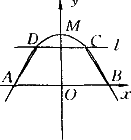
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
目前国内最大跨径的钢管混凝土拱桥——永和大桥,是南宁市又一标志性建筑,其拱形为抛物线的一部分(如图1所示),在正常情况下,位于水面上的桥拱跨度为350米,拱高85米.
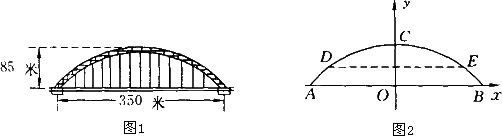
(1)在所给的直角坐标系中(如图2所示),假设抛物线的解析式为y=ax2+b,请你根据上述数据求出a,b的值,并写出抛物线的表达式;(不要求写自变量的取值范围,a,b的值保留两个有效数字)
(2)七月份汛期将要来临,当邕江水位上涨后,位于水面上的桥拱跨度将会减小,当水位上涨4米时,位于水面上的桥拱跨度有多大?(结果保留整数)
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如下图所示,有一座抛物线形拱桥,正常水位时水面宽为20 m,拱顶离水面4 m,在正常水位的基础上,当水位上升h m时,桥下水面宽为d m,在平面直角坐标系中表示B,D两点的坐标.
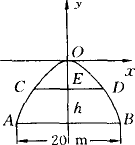
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴轴上,OA=10,OC=6.
(1)如图1所示,在OA上选取一点G,将△COG沿CG翻折,使点O落在BC边上,记为E,求折痕CG所在直线的解析式.

(2)如图2所示,在OC上选取一点D,将△AOD沿AD翻折,使点O落在BC边上,记为![]() .
.
①求折痕AD所在直线的解析式;
②再作![]() F∥AB,交AD于点F,若抛物线y=-
F∥AB,交AD于点F,若抛物线y=-![]() x2+h过点F,求此抛物线的解析式,并判断它与直线AD交点的个数.
x2+h过点F,求此抛物线的解析式,并判断它与直线AD交点的个数.
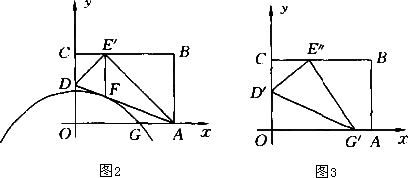
(3)如图3所示,一般地,在OC,OA上选取适当的点![]() ,
,![]() ,使纸片沿
,使纸片沿![]()
![]() 翻折后,点O落在BC边上,记为
翻折后,点O落在BC边上,记为![]() ,请你猜想折痕
,请你猜想折痕![]()
![]() 所在直线与(2)中的抛物线会有什么关系,用(1)中的情形验证你的猜想.
所在直线与(2)中的抛物线会有什么关系,用(1)中的情形验证你的猜想.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如下图所示的是我市一条高速公路上的隧道口在平面直角坐标系内的示意图,点A和A1,点B和B1分别关于y轴对称,隧道部分BCB1为一段抛物线,点B离路面的距离为6米,最高点C离路面AA1的距离为8米,隧道的宽AA1为16米.
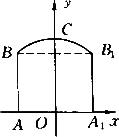
(1)求隧道拱抛物线BCB1的函数解析式;
(2)现有一大型运货车,装载某大型设备后,其宽为4米,大型设备的顶部与路面的距离均为7米,它能否完全通过此隧道?说明理由.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如图所示,一单杠高2.2 m,两立柱之间的距离为1.6 m,将一根绳子拴于立柱与单杠结合处,绳自然下垂呈抛物线状.
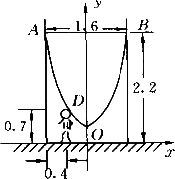
(1)一身高0.7 m的小孩站在离立柱0.4 m处,其头部刚好接触上绳子,求绳子最低点到地面的距离;
(2)为供孩子们打秋千,把绳子剪断后,中间系一块长为0.4 m的木板,除掉系木板用去的绳子后,两边的绳子正好各为2 m,木板与地面平行,求这时木板到地面的距离.(供选用数据:![]() ≈1.8,
≈1.8,![]() ≈1.9,
≈1.9,![]() ≈2.1)
≈2.1)
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
去年冬季我国内蒙部分牧区遭受严重雪灾,空军某部奉命赴灾区空投救灾物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线的顶点在机舱舱口A处,如下图所示.
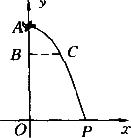
(1)如果空投物资离开A处后下落的垂直高度AB=160米时,它到A处的水平距离BC=200米,那么要使飞机在垂直高度AO=1千米的高空进行空投,物资恰好准确落在居民点P处,则飞机到P处的水平距离OP应为多少米?
(2)如果根据空投的实际风力及风向测算,当空投物资离开A处的垂直距离为160米时,它到A处的水平距离增加至400米,要使飞机仍在(1)中O点的正上方进行空投,且使空投物资准确落在P处,那么飞机空投时离地面的高度应调整为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com