
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
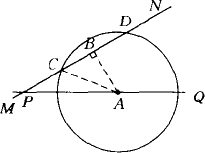
如下图所示,公路MN和公路PQ在点P处交汇,且∠QPN=30°.点A处有一所中学,AP=160米,假设拖拉机行驶时,周围100米以内会受到噪音的影响,那么拖拉机在公路上沿PN方向行驶时,学校是否会受到噪音影响?请说明理由;如果受影响,那么受影响的时间为多少秒?(拖拉机的速度是18千米/时)
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如图所示,二次函数y=x2+bx-c的图象与x轴只有一个公共点P,与y轴的交点为Q,过点Q的直线y=2x+m与x轴交于点A,与这个二次函数的图象交于另一点B,若S△BPQ=3S△APQ,求这个二次函数的解析式.
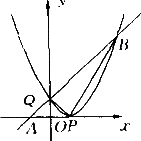
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如图所示,已知A,B两点的坐标分别为(28,0)和(0,28),动点P从A点开始在线段AO上以每秒3个单位的速度向原点O运动,动直线EF从x轴开始以每秒1个单位的速度向上平移(即EF∥x轴),并且分别与y轴、线段AB交于点E,F,连接FP,设动点P与动直线EF同时出发,运动时间为t s.
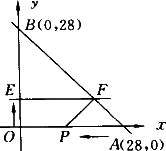
(1)当t=1时,求梯形OPFE的面积,t为何值时,梯形OPFE的面积最大?最大面积是多少?
(2)当梯形OPFE的面积等于△APF的面积时,求线段PF的长;
(3)设t的值分别取t1,t2时(t1≠t2),对应的三角形分别为△AF1P1和△AF2P2,试判断这两个三角形是否相似,请证明你的结论.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
某广告公司欲设计一幅周长为12米的矩形广告牌,广告设计费为每平方米1000元,设矩形一边长为x米,面积为S平方米.
(1)求出S与x之间的函数关系式,并确定自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最高,并求出这个费用;
(3)为使广告牌美观、大方,要求做成黄金矩形,请你按要求设计,并计算出可获得的设计费是多少.(精确到1元)
参考资料:①当矩形的长是宽与(长+宽)的比例中项时,这样的矩形叫做黄金矩形.②![]() ≈2.236.
≈2.236.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如下图所示,抛物线y=ax2+bx+c经过A(-1,0),B(0,-3),C(3,0)三点.

(1)求抛物线的解析式;
(2)若抛物线的顶点为D,求sin∠BOD的值.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
已知c<0,且满足![]() =|2c+1|,抛物线y=ax2+bx+c经过正比例函数y=-4x与反比例函数y=-
=|2c+1|,抛物线y=ax2+bx+c经过正比例函数y=-4x与反比例函数y=-![]() 的图象的交点.
的图象的交点.
(1)求抛物线的解析式;
(2)若抛物线的顶点在直线y=mx+n上,此直线与x轴、y轴分别交于点A,B,且OA∶OB=1∶2,求作一个以m和n为根的二次项系数为1的一元二次方程.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
已知抛物线y=-![]() x2+(6-
x2+(6-![]() )x+m-3与x轴有A,B两个交点,且A,B两点关于y轴对称.
)x+m-3与x轴有A,B两个交点,且A,B两点关于y轴对称.
(1)求m的值;
(2)写出抛物线的解析式及顶点坐标;
(3)根据二次函数与一元二次方程的关系将此题的条件换一种说法写出来.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
已知抛物线y=ax2+bx+c开口向下,且经过A(0,1)和M(2,-3)两点.
(1)若抛物线的对称轴为直线x=-1,求抛物线的解析式;
(2)如果抛物线的对称轴在y轴的左侧,试求a的取值范围;
(3)如果抛物线与x轴交于B,C两点,且∠BAC=90°,求此时a的值.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
已知二次函数y=x2+(2m+1)x+m2的图象与x轴有两个交点.
(1)求m的取值范围;
(2)当这两个交点的横坐标的平方和等于7时,求m的值.
查看答案和解析>>
科目: 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
m在什么范围内取值时,二次函数y=x2-2mx+m2-1的图象与x轴的两个交点都在-2与4之间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com